Chapter 1
Problem Solving: Advanced Principles
Chapters deal specifically with DS issues.
This chapter outlines broad principles for solving advanced PS problems. You've already seen very basic versions of the first three principles in the Introduction, in the dialogues between the Top-Down and the Bottom-Up brain.
As mentioned earlier, these principles draw on the work of George Polya, who was a brilliant mathematician and teacher of mathematics. Polya was teaching future mathematicians, not GMAT test-takers, but what he said still applies. His little book How To Solve It has never been out of print since 1945it's worth getting a copy.
In the meantime, keep reading!
Principle #1: Understand the Basics
Slow down on difficult problems. Keep three broad activities in mind while trying to Understand the problem:
Glance Read Jot
Glance at the entire problem: is it PS or DS? If it's PS, glance at the answer choices to see what form they're in. If it's DS, glance at the statements: is most of the complexity in the question stem or in the statements?
Polya recommended that you ask yourself a few simple questions as you Read a problem. We whole-heartedly agree. Here are some great Polya-style questions that can help you Understand:
- What exactly is the problem asking for?
- What are the quantities I care about? These are often the unknowns.
- What do I know? This could be about certain quantities or about the situation more generally.
- Whatdon'tI know?
- Sometimes you care about something you don't know. This could be an intermediate unknown quantity that you didn't think of earlier.
- Other times, you don't know something, and you don't care. For instance, if a problem includes the quantity 11! (11 factorial), you will practically never need to know the exact value of that quantity.
- What is this problem testing? In other words, why is this problem on the GMAT? What aspect of math are they testing? What kind of reasoning do they want me to demonstrate?
Don't forget to Jot down any given numbers or formulas on your scrap paper.
The Understand the Basics principle applies later on as well. If you get stuck, go back to basics. Re-read the problem and ask yourself these questions again (within a reasonable amount of time, of course).
Start the following problem by trying to Understand what's going on.
Try-It #1-1
x = 910 317 and  is an integer. If n is a positive integer that has exactly two factors, how many different values for n are possible?
is an integer. If n is a positive integer that has exactly two factors, how many different values for n are possible?
| (A) One | (B) Two | (C) Three | (D) Four | (E) Five |
Glance. This is a PS problem. The answers are numbers but in written form; this format is reserved for questions that ask for the number of numbers or number of possibilities for something. The numbers are small.
Read. Dive into the text. Here are some possible answers to the Polya questions.
| What exactly is the problem asking for? | The number of possible values for n.
This means that n might have multiple possible values. In fact, it probably can take on more than one value.
I may not need these actual values. I just need to count them. |
| What are the quantities I care about? | I'm given x and n as variables. These are the quantities I care about. |
| What do I know? | x = 910 317
That is, x = a specific large integer, expressed in terms of powers of 9 and 3.  is an integer. is an integer.
That is, x is divisible by n, or n is a factor of x. Finally, n is a positive integer that has exactly two factors. Prime numbers have exactly two factors. So I can rephrase the information: n is prime. (Primes are always positive.). |
| Whatdon'tI know? | Here's something I don't know: I don't know the value of x as a series of digits. Using a calculator or Excel, I could find out that x equals 3,357,644,238. But I don't know this number at the outset. Moreover, because this calculation is far too cumbersome, it must be the case that I don't need to find this number. |
| What is this problem testing? | From the foregoing, I can infer that this problem is testing Divisibility & Primes. I will probably also need to manipulate exponents, since I see them in the expression for x. |
You can ask these questions in whatever order is most helpful for the problem. For instance, you might not look at what the problem is asking for until you've understood the given information.
Jot. As you decide that a piece of information is important, jot it down on your scrap paper. At this point, your scrap paper might look something like this:
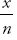 = int n = prime
= int n = prime
x = 910 317
Principle #2: Build a Plan
Next, think about how you will solve the problem.
Reflect Organize
Reflect. Here are some Polya questions that help you think about what you know and come up with a Plan.
| Is a good approach already obvious? | From your answers above, you may already see a way to reach the answer. If you can envision the rough outlines of the right path, then go ahead and get started. |
| If not, what in the problem can help me figure out a good approach? | If you are stuck, look for particular clues to tell you what to do next. Revisit your answers to the basic questions. What do those answers mean? Can you rephrase or reword them? Can you combine two pieces of information in any way, or can you rephrase the question, given everything you know? |
| Can I remember a similar problem? | Try relating the problem to other problems you've faced. This can help you categorize the problem or recall a solution process. |
Organize. For the Try-It #1-1 problem, some of the information is already rephrased (re-organized). Go further now, combining information and simplifying the question.
| Given: | n is a prime number AND n is a factor of x |
| Combined: | nis a prime factor ofx |
| Question: | How many different values for n are possible? |
| Combined: | How many different values for n, a prime factor ofx, are possible? |
| Rephrased: | How many distinct prime factors doesxhave? |
You need the prime factorization of x. Notice that n is not even in the question anymore. The variable n just gave you a way to ask this underlying question.
Consider the other given fact: x = 910 317. It can be helpful initially to put certain complicated facts to the side. At this stage, however, you know that you need the prime factors of x. So now you have the beginning of a plan: factor this expression into its primes.
Principle #3: Solveand Put Pen to Paper
The third step is to do the work: Solve.
Work














 is an integer. If n is a positive integer that has exactly two factors, how many different values for n are possible?
is an integer. If n is a positive integer that has exactly two factors, how many different values for n are possible? is an integer.
is an integer.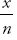 = int n = prime
= int n = prime