Number systems
Here you can read online Number systems full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2016, publisher: The Open University, genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
Number systems: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Number systems" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Unknown: author's other books
Who wrote Number systems? Find out the surname, the name of the author of the book and a list of all author's works by series.
Number systems — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Number systems" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Font size:
Interval:
Bookmark:
About this free course
This free course is an adapted extract from the Open Unviersity course M208: Pure Mathematics www3.open.ac.uk/study/undergraduate/course/m208.htm
This version of the content may include video, images and interactive content that may not be optimised for your device.
You can experience this free course as it was originally designed on OpenLearn, the home of free learning from The Open University: www.open.edu/openlearn/science-maths-technology/mathematics-and-statistics/mathematics/number-systems/content-section-0.
There youll also be able to track your progress via your activity record, which you can use to demonstrate your learning.
The Open University, Walton Hall, Milton Keynes, MK7 6AA
Copyright 2016 The Open University
Intellectual property
Unless otherwise stated, this resource is released under the terms of the Creative Commons Licence v4.0 http://creativecommons.org/licenses/by-nc-sa/4.0/deed.en_GB. Within that The Open University interprets this licence in the following way: www.open.edu/openlearn/about-openlearn/frequently-asked-questions-on-openlearn. Copyright and rights falling outside the terms of the Creative Commons Licence are retained or controlled by The Open University. Please read the full text before using any of the content.
We believe the primary barrier to accessing high-quality educational experiences is cost, which is why we aim to publish as much free content as possible under an open licence. If it proves difficult to release content under our preferred Creative Commons licence (e.g. because we cant afford or gain the clearances or find suitable alternatives), we will still release the materials for free under a personal end-user licence.
This is because the learning experience will always be the same high quality offering and that should always be seen as positive even if at times the licensing is different to Creative Commons.
When using the content you must attribute us (The Open University) (the OU) and any identified author in accordance with the terms of the Creative Commons Licence.
The Acknowledgements section is used to list, amongst other things, third party (Proprietary), licensed content which is not subject to Creative Commons licensing. Proprietary content must be used (retained) intact and in context to the content at all times.
The Acknowledgements section is also used to bring to your attention any other Special Restrictions which may apply to the content. For example there may be times when the Creative Commons Non-Commercial Sharealike licence does not apply to any of the content even if owned by us (The Open University). In these instances, unless stated otherwise, the content may be used for personal and non-commercial use.
We have also identified as Proprietary other material included in the content which is not subject to Creative Commons Licence. These are OU logos, trading names and may extend to certain photographic and video images and sound recordings and any other material as may be brought to your attention.
Unauthorised use of any of the content may constitute a breach of the terms and conditions and/or intellectual property laws.
We reserve the right to alter, amend or bring to an end any terms and conditions provided here without notice.
All rights falling outside the terms of the Creative Commons licence are retained or controlled by The Open University.
Head of Intellectual Property, The Open University
Designed and edited by The Open University
978-1-4730-1383-4 (.kdl)
978-1-4730-0615-7 (.epub)
In this course we look at some different systems of numbers, and the rules for combining numbers in these systems. For each system we consider the question of which elements have additive and/or multiplicative inverses in the system. We look at solving certain equations in the system, such as linear, quadratic and other polynomial equations.
In Section 1 we start by revising the notation used for the rational numbers and the real numbers, and we list their arithmetical properties. You will meet other properties of these numbers in the analysis units, as the study of real functions depends on properties of the real numbers. We note that some quadratic equations with rational coefficients, such as x2 = 2, have solutions which are real but not rational.
In Section 2 we introduce the set of complex numbers. This system of numbers enables us to solve all polynomial equations, including those with no real solutions, such as x2 + 1 = 0. Just as real numbers correspond to points on the real line, so complex numbers correspond to points in a plane, known as the complex plane.
In Section 3 we look further at some properties of the integers, and introduce modular arithmetic. This will be useful in the group theory units, as some sets of numbers with the operation of modular addition or modular multiplication form groups.
In Section 4 we introduce the concept of a relation between elements of a set. This is a more general idea than that of a function, and leads us to a mathematical structure known as an equivalence relation. An equivalence relation on a set classifies elements of the set, separating them into disjoint subsets called equivalence classes.
This OpenLearn course is an adapted extract from the Open Unviersity course M208: Pure Mathematics
After studying this course, you should be able to:
- understand the arithmetical properties of the rational and real numbers
- understand the definition of a complex number
- perform arithmetical operations with complex numbers
- explain the terms modular addition and modular multiplication
- explain the meanings of a relation defined on a set, an equivalent relation and a partition of a set.
In OpenLearn course M208_5 Mathematical language you met the sets
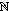 = {1, 2, 3, }, the natural numbers;
= {1, 2, 3, }, the natural numbers;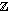 = {, 2, 1, 0, 1, 2, }, the integers;
= {, 2, 1, 0, 1, 2, }, the integers;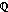 = {p/q : p
= {p/q : p
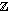 , q
, q
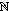 }, the rational numbers.
}, the rational numbers.
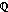 is the set of numbers that can be written as fractions, such as
is the set of numbers that can be written as fractions, such as  and 1.7 =
and 1.7 = 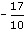 .
.
Notice that each set in this list is a subset of the succeeding one; that is,

To represent the rational numbers geometrically, we use a number line. We begin by drawing a line and marking on it points corresponding to the integers 0 and 1. If the distance between 0 and 1 is taken as a unit of length, then the rational numbers can be arranged on the line in a natural order. For example, the rational 4/3 is placed at the point which is one third of the distance from 1 to 2.
Font size:
Interval:
Bookmark:
Similar books «Number systems»
Look at similar books to Number systems. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
Discussion, reviews of the book Number systems and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.












