Ivor Horton [Ivor Horton] - Ivor Horton’s Beginning Java®, Java 7 Edition

ABOUT THE AUTHOR

IVOR HORTON started out as a mathematician, but shortly after graduating, he was lured into messing about with computers by a well-known manufacturer. He has spent many happy years programming occasionally useful applications in a variety of languages as well as teaching mainly scientists and engineers to do likewise. He has extensive experience in applying computers to problems in engineering design and to manufacturing operations in a wide range of industries. He is the author of a number of tutorial books on programming in C, C++, and Java. When not writing programming books or providing advice to others, he leads a life of leisure.

ABOUT THE TECHNICAL EDITORS

MARC GREGOIRE is a software engineer from Belgium. He graduated from the Catholic University of Leuven, Belgium, with a degree in Burgerlijk ingenieur in de computer wetenschappen (equivalent to master of science in engineering in computer science). The year after, he received the cum laude degree of master in artificial intelligence at the same university. After his studies, Marc started working for a big software consultancy company called Ordina Belgium. As a consultant, he worked for Siemens and Nokia Siemens Networks on critical 2G and 3G software running on Solaris for big telecom operators. This required working in international teams stretching from South America and USA to EMEA and Asia. Now, Marc is working for Nikon Metrology on 3D scanning software.

His main expertise is C/C++, and specifically Microsoft VC++ and the MFC framework. Next to C/C++, Marc also likes C# and uses PHP for creating web pages. In addition to his main interest for Windows development, he also has experience in developing C++ programs running 24x7 on Linux platforms; for example, EIB home automation controlling and monitoring software. Since April 2007, hes received the yearly Microsoft MVP (Most Valuable Professional) award for his Visual C++ expertise.

Marc is an active member on the CodeGuru forum (as Marc G) and wrote some articles and FAQ entries for CodeGuru. He also creates freeware and shareware programs that are distributed through his website at www.nuonsoft.com , and maintains a blog on www.nuonsoft.com/blog/ .

AL SCHERER is a Development Manager of eCommerce Technologies at Follett Higher Education Group. He has seven years of experience designing and coding applications as a Software Architect in addition to 10 years of development experience. Al has built applications using Assembler, C, C++ and a number of other programming languages and has worked extensively in Java since Version 1.1. He holds Sun Java certifications as a Programmer, Business Components Developer and Web Components Developer. In his spare time, Al applies his passion for technology via technical writing and editing, working on nine software books over the last few years. He holds a BS in Engineering from University of Illinois at Urbana-Champaign and an MBA from Northwestern University.

ACKNOWLEDGMENTS

OF COURSE THIS BOOK is not all my own work. The John Wiley & Sons, and Wrox Press editorial and production team transformed my draft into the finished book. Im especially indebted to Project Editor Maureen Spears, who has been there from way back at the beginning and has been incredibly helpful throughout. Charlotte Kughen has done a great job of untangling my grammar and identifying my sometimes obscure references. Id like to thank the Technical Editors for their thorough review of the text and checking out all the examples in the book; their many constructive comments undoubtedly helped make the book much better that it would otherwise have been.

As always, the love and support of my wife Eve has been essential for me to finish this book. She remains patient and cheerful, even when I am not necessarily the same.

A

Keywords

The following keywords are reserved in Java, so you must not use them as names in your programs:

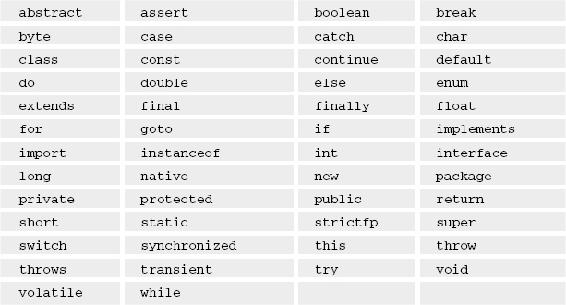
Although they are not keywords, you should not use the boolean values true and false or the value null as names in your programs.

Note that const and goto have not been used in the Java language up to now, but they are still reserved words and you must not use them as names.

B

Computer Arithmetic

In the chapters of this book, I have deliberately kept discussion of binary arithmetic to a minimum. However, it is important overall, and fundamental to understanding how some operators work, so Im including a summary of the subject in this appendix. If you feel confident about your math knowledge, this is all old hat to you and you need read no farther. If you find the math parts tough, then this appendix should show you how easy it really is.

BINARY NUMBERS

First lets consider what you mean when you write a common everyday number such as 321 or 747. Put more precisely you mean

321 is:

3 (10 10) + 2 (10) + 1

and 747 is:

7 (10 10) + 4 (10) + 7

Because it is built around powers of ten, you call this the decimal system (derived from the Latin decimalis , meaning of tithes , which was a tax of 10 percent ah, those were the days...).

Representing numbers in this way is very handy for people with ten fingers and ten toes, or creatures with ten of any kind of appendage for that matter. However, your PC is quite unhandy in this context, being built mainly of switches that are either on or off. This is okay for counting up to two, but not spectacular at counting to ten. For this reason your computer represents numbers to base 2 rather than base 10. This is called the binary system of counting, analogous to the bi cycle (two wheels), but nothing whatever to do with bibacity, which means an inclination to drink a lot. With the decimal system, to base 10, the digits used can be from 0 to 9. In the binary system, to base 2, the digits can only be 0 or 1, ideal when you have only on/off switches to represent them; off is usually 0, and on is 1 simple. Each digit in the binary system is called a bit , which is a contraction of binary digit. In an exact analogy to the usual base 10 counting, the binary number 1101 is therefore:

1 (2 2 2) + 1 (2 2) + 0 (2) + 1

which, if you work it out, amounts to 13 in the decimal system. In , you can see the decimal equivalents of 8-bit binary numbers illustrated.

Decimal Equivalents of 8-bit Binary Numbers

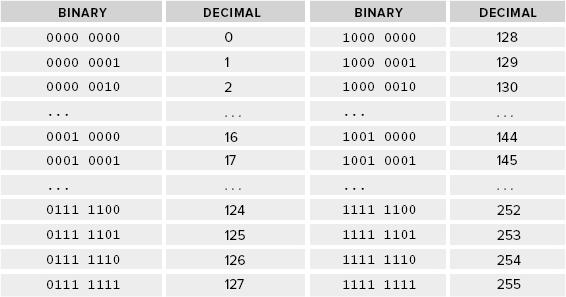
Note that by using just 7 bits, you can represent all the decimal numbers from 0 to 127, which is a total of 2, or 128 numbers; and using all 8 bits you get 256, which corresponds to 2 numbers. In general, if you have n bits available, you can represent 2 n positive integers with values from 0 to 2 n . Of course, I am only talking in the context positive numbers so far. If you also need the same number of negative numbers, you need more bits. I get to negative numbers in a moment.

Hexadecimal Numbers

When you get to work with larger binary numbers for example, numbers with 24 bits:

1111 0101 1011 1001 1110 0001

the notation starts to be a little cumbersome, particularly when you consider that if you apply the method you saw in the previous section to work out what this is in decimal notation, its only 16,103,905, a miserable 8 decimal digits. You can sit more angels on a pinhead than that. Well, as it happens, you have an excellent alternative.

Arithmetic to base 16 is a very convenient option. Numbers to base 16 are hexadecimal numbers. Each digit can have values from 0 to 15 (the digits from 10 to 15 being represented by the letters A to F as shown in , or by a to f if youre averse to capitalization) and values from 0 to 15 correspond quite nicely with the range of values that four binary digits can represent.