Alfred S. Posamentier et al. - The Joy of Mathematics: Marvels, Novelties, and Neglected Gems That Are Rarely Taught in Math Class

The authors wish to acknowledge superb support services received from the publisher Prometheus Books, led by their editor in chief, Steven L. Mitchell, and his truly dedicated production coordinator, Catherine Roberts-Abel. We wish to also thank Senior Editor Jade Zora Scibilia for her highly meticulous editing and clever suggestions to make the presentation as intelligible as possible. Thanks is also due to Editorial Assistant Hanna Etu, and the typesetter, Bruce Carle. The cover design exhibits the talents of Nicole Sommer-Lecht. We're also very pleased with the indexing by Laura Shelley.

Each of the authors has many people to thank for their patience and support throughout this book-development process. In particular, Dr. Christian Spreitzer wants to thank Katharina Brazda for inspiring discussions, which resulted in some very creative contributions.

As we mentioned earlier, Ceva's theorem might well have been introduced to a high school class, since it merely applies similarity relationships that are an integral part of the geometry curriculum. We offer one of many proofs available to justify Ceva's theorem. It is perhaps easier to follow the proof by looking at the left-side diagram in and then verifying the validity of each of the statements in the right-side diagram. In any case, the statements made in the proof hold for both diagrams.

Figure App.1.

Consider , for which we have on the left triangle ABC with a line (SR) containing A and parallel to BC, intersecting CP extended at S and BP extended at R.

The parallel lines enable us to establish the following pairs of similar triangles:

Now by multiplying (I), (II), and (V), we obtain our desired result:

This can also be written as AMBNCL = MCNABL. A nice way to read this theorem is that the product of the alternate segments along the sides of the triangle made by the concurrent line segments (called cevians) emanating from the triangle's vertices and ending at the opposite side are equal.

Yet, it is the converse of this proof that is of particular value to use here. That is, if the products of the alternate segments along the sides of the triangle are equal, then the cevians determining these points must be concurrent.

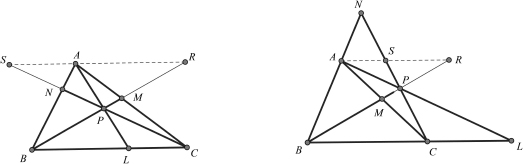
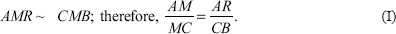
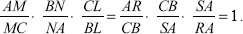
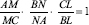We shall now prove that if the lines containing the vertices of triangle ABC intersect the opposite sides in points L, M, and N, respectively, so that , then these lines, AL, BM, and CN, are concurrent.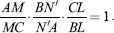

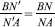Suppose BM and AL intersect at P. Draw PC and call its intersection with AB point N'. Now that AL, BM, and CN' are concurrent, we can use the part of Ceva's theorem proved earlier to state the following:

But our hypothesis stated that .

Therefore, , so that N and N must coincide, which thereby proves the concurrency.

For convenience, we can restate this relationship as follows: If AMBNCL = MCNABL, then the three lines are concurrent.

The ambitious reader may want to see other proofs of Ceva's theorem, which can be found in Advanced Euclidean Geometry by Alfred S. Posamentier (New York: John Wiley and Sons, 2002, pp. 2731.

When you think of arithmetic, you typically consider the four basic arithmetic operations. With a little more thought, you tend to tag on the square root operation as well. Unfortunately, most of our school curriculum focuses on ensuring that we have a good mechanical command of the arithmetic operations and know the number facts as best we can to service us efficiently in our everyday life. As a result, most adults are not aware of the many amazing relationships that can be exhibited arithmetically with numbers. Some of these can be extremely useful in our everyday life as well. For example, just by looking at a number and determining if it is divisible by 3, 9, or 11 can be very useful, especially if it can be done at a glance. When it involves determining divisibility by 2, we do this without much thought, by simply inspecting the last digit. We shall extend this discussion to considering divisibility by a prime number, something that clearly is not presented in the school curriculum, with which we hope to motivate the reader to investigate further primes beyond those shown here. We truly expect that the wonders that our number system holds, many of which we will present in this book, will motivate you to search for more of these curiosities along with their justifications. Some of the units in this chapter will also provide you with a deeper understanding for our number system beyond merely arithmetic manipulations. Our introduction to a variety of special numbers will generate a greater appreciation of arithmetic than the typical school courses provide. Let us begin our journey through numbers and their operations.

WHEN IS A NUMBER DIVISIBLE BY 3 OR 9?

Teachers at various grade levels often neglect to mention to students that in order to determine whether a number is divisible by 3 or 9, you just have to apply a simple rule: If the sum of the digits of a number is divisible by 3 (or 9), then the original number is divisible by 3 (or 9).

An example will best firm up your understanding of this rule. Consider the number 296,357. Let's test it for divisibility by 3 (or 9). The sum of the digits is 2 + 9 + 6 + 3 + 5 + 7 = 32, which is not divisible by 3 or 9. Therefore, the original number, 296, 357, is not divisible by 3 or 9.

Now suppose the number we consider is 457,875. Is it divisible by 3 or 9? The sum of the digits is 4 + 5 + 7 + 8 + 7 + 5 = 36, which is divisible by 9 (and then, of course, divisible by 3 as well), so the number 457,875 is divisible by 3 and by 9. If by some remote chance it is not immediately clear to you whether the sum of the digits is divisible by 3 or 9, then continue with this process; take the sum of the digits of your original sum and continue adding the digits until you can visually make an immediate determination of divisibility by 3 or 9.