Alex Bellos - Can You Solve My Problems?: A Casebook of Ingenious, Perplexing and Totally Satisfying Puzzles

All my problems began with Cheryl.

She was a complicated girl. A real tease.

But I couldnt stop thinking about her. And in many ways she changed the course of my life.

I should clarify here that Cheryl doesnt exist. She was the protagonist in a question from a Singaporean maths exam that captured my imagination, seducing me into exploring a world of puzzles that led to this book.

You will find the Cheryls Birthday problem and the full story of our relationship later in this book. (Its Problem 21, and appears on page 41.) But before we embark on our journey through my favourite mathematical puzzles, here are two appetite-whetting amuse-brains.

First, look at the image below. The numbers are arranged according to a certain rule. Once youve worked out the rule, fill in the missing number. The number seven in the final circle is not a typographical error.

I find this puzzle irresistible. It looks intriguing. It requires no advanced mathematics. It taunts you to solve it, and when you do (if you do) the sense of satisfaction is both exhilarating and addictive. Nob Yoshigahara, a celebrated twentieth-century Japanese puzzle inventor, considered it his masterpiece. Try to work out the answer before I reveal it, at the end of this section.

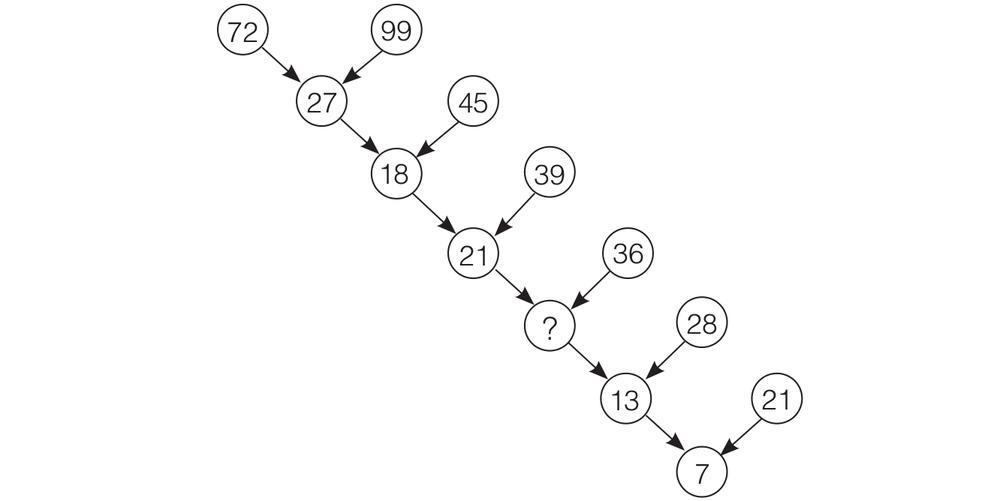
Second, the Canals on Mars. A map of the red planet displays newly discovered cities and waterways. Start at the city T on the south pole. Travelling along the canals, visiting each city only once and returning to the starting point, can you spell out a sentence in English?

This problem, by the prolific American puzzle inventor Sam Loyd, is more than a hundred years old. He wrote that when the puzzle originally appeared in a magazine, more than fifty thousand readers reported There is no possible way. Yet it is a very simple puzzle. You will kick yourself if you read the answer before you work it out.

* * *

If you paused to tackle either of these two problems I hardly need explain why puzzles are so enjoyable. They reel you in. Distractions around you disappear as you focus in on the solution. Being forced to use your wits is life-affirming. And deductive reasoning in simple logical steps is comforting, especially when real life is often so illogical. Good puzzles also present achievable goals, which are supremely gratifying when they come.

One consequence of my tryst with Cheryl was that I began to write an online puzzle column for the Guardian. In order to find the best possible puzzles I immersed myself in books and corresponded with both amateur and professional puzzlesmiths. I have always loved mathematical puzzles, but before I began this research I had not fully appreciated their variety, conceptual depth and rich history. I did not realise, for example, that one thousand years ago the main role of mathematics with the exception of dull commercial tasks like counting and measuring was to provide intellectual diversion and amusement. (Arguably, the statement remains true today, given that the number of Sudoku enthusiasts vastly exceeds the number of professional mathematicians.) Puzzles form a parallel history of mathematics, reflecting great discoveries and inspiring the sharpest minds.

This book is a curated collection of 125 brainteasers from the last two millennia, linked with stories about their origins and influence. I have chosen the puzzles that I found most fascinating, entertaining and thought-provoking. They are mathematical only in the widest possible sense: the solutions require logical thought, but they do not require advanced maths. The problems come from ancient China, medieval Europe, Victorian England and modern-day Japan, as well as other ages and places. Some are traditional riddles, others were devised by the top professional mathematicians of their day. Often, however, its hard to say where a puzzle comes from. Like jokes and folk tales, they are always evolving as each new generation embellishes, adapts, simplifies, extends and restyles them.

The best puzzles are pieces of poetry. With elegance and brevity, they pique our interest, kindle our competitive spirit, test our ingenuity, and in some cases reveal universal truths. A good puzzle requires no specialist knowledge only creativity, cunning and an ability to think clearly. Puzzles are captivating because they appeal to the human impulse to make sense of the world; they give us pleasure because we are making sense out of something. Yet no matter how frivolous or contrived a puzzle may be, the strategies we use to solve them expand our armoury for tackling other challenges in life.

Most importantly, however, puzzles indulge our intellectual playfulness. They are fun. They reflect a childlike sense of curiosity. Ive chosen puzzles in as many styles as possible, and which require us to think in very different ways. Some rely on a flash of insight, some require us to follow our noses, and others well, that would be telling.

Each chapter has a theme, and its problems appear roughly in chronological order. The questions are not in order of difficulty. Level is often hard to judge, anyway. Whats torture for one person may be trivial for another, and vice versa. I explain how to solve a few puzzles, and give tips for a few more, but for the rest youre on your own. (The answers are at the back of the book.) Some of my problems are simple. Some will have you scratching your head for days. These toughies are signposted with the symbol 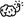. If you fail to crack them I hope you will find the solutions just as fascinating as the problems themselves. Sometimes the thrill is in learning a technique, an idea, or its consequences, that you did not know.

Before each chapter I have included ten quick-fire questions to get you in the mood. The first, third and fifth contain questions, of increasing difficulty, used by the United Kingdom Mathematics Trust in their annual national challenges for students aged 11 to 13. Thats right, ten questions forchildren. Are you up to it?

Now back to those questions I asked at the start.

When you look at the number tree your eye goes to the top left. How can 72 and 99 make 27?

Got it! 99 72 = 27.

In other words, the number in a circle is the difference of the numbers in the two circles that point to it.

And look, the same pattern follows with 18, the next number down the line:

45 27 = 18

And with 21 too:

39 18 = 21

Which means that the missing number must be the difference between 21 and 36, which is 15:

36 21 = 15

For completenesss sake, we continue down the tree:

28 15 = 13

Nice! So it continues to work. Were almost there.

Until BOOM.

The very last number is 7, which is not the difference between 13 and 21, the two numbers pointing to it.

Dammit! Our original supposition is wrong. It is not the case that a number in a circle is equal to the difference of the two numbers pointing to it. Yoshigahara has artfully led us down the garden path, only to trip us up at the end of it.