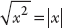Manhattan Prep
GRE Flash Cards: 500 Math Flash Cards Copyright 2013 MG Prep, Inc.
ALL RIGHTS RESERVED. No part of this work may be reproduced or used in any form or by any meansgraphic, electronic, or mechanical, including photocopying, recording, taping, Web distributionwithout the prior written permission of the publisher, MG Prep Inc. Note: GRE, Graduate Record Examination, Educational Testing Services, and ETS are all registered trademarks of Educational Testing Services, which neither sponsors nor is affiliated in any way with this product. If both
x and
y are odd, is
xy odd? Answer: Yes,
xy is odd. We could just recall: an odd number times an odd number is always odd. If you want proof, notice that odd numbers can be represented as 2
m + 1 or 2
n + 1, where
m and
n are integers.
Multiplying two numbers of this form together would yield 4nm + 2m + 2n + 1, which is always odd. The 1st, 2nd, and 3rd terms are multiplied by 2 (or 4), so they are even, as is their sum. An even number plus one is odd. Thus xy is odd. When in doubt, try it out! Pick numbers to test properties.  If xy2 < 0, is x < 0? Answer: Yes.
If xy2 < 0, is x < 0? Answer: Yes.
Any number, except for 0, raised to an even power will be positive. If y were 0, the inequality would not be true, so we know that y2 will be positive. For xy2 to be less than zero, x must be negative. Simplify 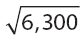 . Answer:
. Answer: 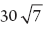 When simplifying an expression under the square root sign, you can factor the expression into primes. In this case, 6,300 = 22 32 52 7.
When simplifying an expression under the square root sign, you can factor the expression into primes. In this case, 6,300 = 22 32 52 7.
For every pair under the square root sign, move one outside the radical, and throw the other away: 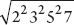 becomes (2)(3)(5)
becomes (2)(3)(5) 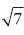 , or simply
, or simply 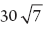 . You can also factor out perfect squares that you notice:
. You can also factor out perfect squares that you notice: 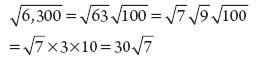 If both x and y are odd, is x2 + y odd? Answer: No, x2 + y is even. x2 = (Odd)2 = Odd x2 + y = Odd + Odd = Even If you want proof, notice that odd numbers can be represented as 2m + 1 or 2n + 1, where m and n are integers. (2m + 1)2 = 4m2 + 4m + 1, and adding 2n + 1 would yield 4m2 + 4m + 2n + 2. This is always even, since a 2 can be factored from all four terms.
If both x and y are odd, is x2 + y odd? Answer: No, x2 + y is even. x2 = (Odd)2 = Odd x2 + y = Odd + Odd = Even If you want proof, notice that odd numbers can be represented as 2m + 1 or 2n + 1, where m and n are integers. (2m + 1)2 = 4m2 + 4m + 1, and adding 2n + 1 would yield 4m2 + 4m + 2n + 2. This is always even, since a 2 can be factored from all four terms. 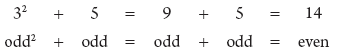 If x is odd and y is even, is xy odd or even? Answer: xy is even. xy = (Odd)(Even) = Even. xy = (Odd)(Even) = Even.
If x is odd and y is even, is xy odd or even? Answer: xy is even. xy = (Odd)(Even) = Even. xy = (Odd)(Even) = Even.
If you want proof, notice that an odd number can be represented as 2m + 1, and an even number can be represented as 2n, where m and n are integers. Multiplying 2m + 1 and 2n would yield 4mn + 2n, which is always even, since 2 is a factor of both terms. (Factor out the 2 to get 2(2mn + n), which shows that this number will be even.) When in doubt, try it out! Pick numbers to test properties. 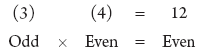 If x13 < 0, is x > 0? Answer: No. Don't let the 13 confuse you; the only thing that matters is that 13 is an odd number. Odd exponents preserve the sign of the base.
If x13 < 0, is x > 0? Answer: No. Don't let the 13 confuse you; the only thing that matters is that 13 is an odd number. Odd exponents preserve the sign of the base.
If x13 < 0, then x is also less than 0. Simplify 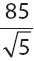 Answer:
Answer: 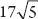 When a square root lurks in the denominator, we can rationalize the denominator by multiplying by the appropriate form of 1in this case,
When a square root lurks in the denominator, we can rationalize the denominator by multiplying by the appropriate form of 1in this case, 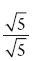 .
. 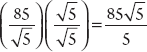 , and 85 divided by 5 is 17, so the simplest form is
, and 85 divided by 5 is 17, so the simplest form is 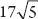 . If both x and y are odd, is xy odd? Answer: No, xy is even. xy = Odd Odd = Even If you want proof, notice that odd numbers can be represented as 2m + 1 or 2n + 1, where m and n are integers. Subtracting two numbers of this form would yield (2n + 1) (2m + 1), or just 2n 2m, which is always even, since a 2 can be factored out of the remaining terms (i.e., 2(nm)).
. If both x and y are odd, is xy odd? Answer: No, xy is even. xy = Odd Odd = Even If you want proof, notice that odd numbers can be represented as 2m + 1 or 2n + 1, where m and n are integers. Subtracting two numbers of this form would yield (2n + 1) (2m + 1), or just 2n 2m, which is always even, since a 2 can be factored out of the remaining terms (i.e., 2(nm)).
When in doubt, try it out! Pick numbers to test properties. 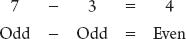 Calculate (1)789. Answer: 1 Since (1) (1) = 1, 1 raised to any even power is 1. If you multiply by 1 one more time, you end up with 1, so 1 raised to any odd power will equal 1. 789 is an odd number, so (1)789 = 1. (1)odd = 1 x is divisible by 42.
Calculate (1)789. Answer: 1 Since (1) (1) = 1, 1 raised to any even power is 1. If you multiply by 1 one more time, you end up with 1, so 1 raised to any odd power will equal 1. 789 is an odd number, so (1)789 = 1. (1)odd = 1 x is divisible by 42.
Which of the following numbers is definitely a factor of x2? Choose all that apply. 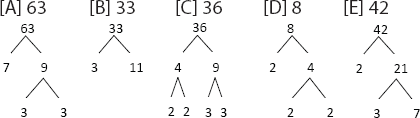 Answer: [A] 63 and [C] 36 If x definitely has 2, 3 and 7 as factors, then when we square x, we know that x2 will have two 2s, two 3s and two 7s as factors. 63 is 7 3 3, and 36 is 2 2 3 3. Using the factors foundation rule, we can guarantee that all numbers that solely use those factors are factors of x2. Both 63 and 36 use only prime factors found in x2.
Answer: [A] 63 and [C] 36 If x definitely has 2, 3 and 7 as factors, then when we square x, we know that x2 will have two 2s, two 3s and two 7s as factors. 63 is 7 3 3, and 36 is 2 2 3 3. Using the factors foundation rule, we can guarantee that all numbers that solely use those factors are factors of x2. Both 63 and 36 use only prime factors found in x2. 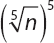 is always equal to which of the following? (A) n (B) n25 (C) n1/5 (D) 1 Answer: (A) n Try it:
is always equal to which of the following? (A) n (B) n25 (C) n1/5 (D) 1 Answer: (A) n Try it: 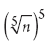 is the same as
is the same as 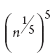 , which is equal to n, since (na)b = nab, and 5 times 1/5 equals 1.
, which is equal to n, since (na)b = nab, and 5 times 1/5 equals 1.
Alternatively, 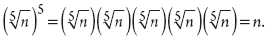 If you need convincing, pick a few numbers and see what happens! Technically, you have to be a little careful with even powers and roots (for instance,
If you need convincing, pick a few numbers and see what happens! Technically, you have to be a little careful with even powers and roots (for instance, 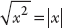
















 If xy2 < 0, is x < 0? Answer: Yes.
If xy2 < 0, is x < 0? Answer: Yes.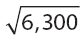 . Answer:
. Answer: 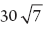 When simplifying an expression under the square root sign, you can factor the expression into primes. In this case, 6,300 = 22 32 52 7.
When simplifying an expression under the square root sign, you can factor the expression into primes. In this case, 6,300 = 22 32 52 7.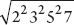 becomes (2)(3)(5)
becomes (2)(3)(5)  , or simply
, or simply  If both x and y are odd, is x2 + y odd? Answer: No, x2 + y is even. x2 = (Odd)2 = Odd x2 + y = Odd + Odd = Even If you want proof, notice that odd numbers can be represented as 2m + 1 or 2n + 1, where m and n are integers. (2m + 1)2 = 4m2 + 4m + 1, and adding 2n + 1 would yield 4m2 + 4m + 2n + 2. This is always even, since a 2 can be factored from all four terms.
If both x and y are odd, is x2 + y odd? Answer: No, x2 + y is even. x2 = (Odd)2 = Odd x2 + y = Odd + Odd = Even If you want proof, notice that odd numbers can be represented as 2m + 1 or 2n + 1, where m and n are integers. (2m + 1)2 = 4m2 + 4m + 1, and adding 2n + 1 would yield 4m2 + 4m + 2n + 2. This is always even, since a 2 can be factored from all four terms.  If x is odd and y is even, is xy odd or even? Answer: xy is even. xy = (Odd)(Even) = Even. xy = (Odd)(Even) = Even.
If x is odd and y is even, is xy odd or even? Answer: xy is even. xy = (Odd)(Even) = Even. xy = (Odd)(Even) = Even. If x13 < 0, is x > 0? Answer: No. Don't let the 13 confuse you; the only thing that matters is that 13 is an odd number. Odd exponents preserve the sign of the base.
If x13 < 0, is x > 0? Answer: No. Don't let the 13 confuse you; the only thing that matters is that 13 is an odd number. Odd exponents preserve the sign of the base.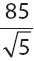 Answer:
Answer: 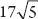 When a square root lurks in the denominator, we can rationalize the denominator by multiplying by the appropriate form of 1in this case,
When a square root lurks in the denominator, we can rationalize the denominator by multiplying by the appropriate form of 1in this case, 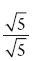 .
. 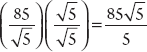 , and 85 divided by 5 is 17, so the simplest form is
, and 85 divided by 5 is 17, so the simplest form is  Calculate (1)789. Answer: 1 Since (1) (1) = 1, 1 raised to any even power is 1. If you multiply by 1 one more time, you end up with 1, so 1 raised to any odd power will equal 1. 789 is an odd number, so (1)789 = 1. (1)odd = 1 x is divisible by 42.
Calculate (1)789. Answer: 1 Since (1) (1) = 1, 1 raised to any even power is 1. If you multiply by 1 one more time, you end up with 1, so 1 raised to any odd power will equal 1. 789 is an odd number, so (1)789 = 1. (1)odd = 1 x is divisible by 42. Answer: [A] 63 and [C] 36 If x definitely has 2, 3 and 7 as factors, then when we square x, we know that x2 will have two 2s, two 3s and two 7s as factors. 63 is 7 3 3, and 36 is 2 2 3 3. Using the factors foundation rule, we can guarantee that all numbers that solely use those factors are factors of x2. Both 63 and 36 use only prime factors found in x2.
Answer: [A] 63 and [C] 36 If x definitely has 2, 3 and 7 as factors, then when we square x, we know that x2 will have two 2s, two 3s and two 7s as factors. 63 is 7 3 3, and 36 is 2 2 3 3. Using the factors foundation rule, we can guarantee that all numbers that solely use those factors are factors of x2. Both 63 and 36 use only prime factors found in x2. 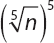 is always equal to which of the following? (A) n (B) n25 (C) n1/5 (D) 1 Answer: (A) n Try it:
is always equal to which of the following? (A) n (B) n25 (C) n1/5 (D) 1 Answer: (A) n Try it: 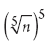 is the same as
is the same as 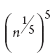 , which is equal to n, since (na)b = nab, and 5 times 1/5 equals 1.
, which is equal to n, since (na)b = nab, and 5 times 1/5 equals 1.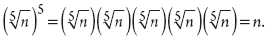 If you need convincing, pick a few numbers and see what happens! Technically, you have to be a little careful with even powers and roots (for instance,
If you need convincing, pick a few numbers and see what happens! Technically, you have to be a little careful with even powers and roots (for instance,