This introductory chapter gathers together some of the most basic tools and notions that are used throughout the book. It also introduces some common vocabulary and notations used in modern mathematical physics literature. Readers familiar with such concepts as sets, maps, equivalence relations, and metric spaces may wish to skip this chapter.
1.1 Sets
Modern mathematics starts with the basic (and undefinable) concept of set . We think of a set as a structureless family, or collection, of objects. We speak, for example, of the set of students in a college, of men in a city, of women working for a corporation, of vectors in space, of points in a plane, or of events in the continuum of space-time. Each member a of a set A is called an element of that set. This relation is denoted by a A (read a is an element of A or a belongs to A ), and its negation by a A . Sometimes a is called a point of the set A to emphasize a geometric connotation.
A set is usually designated by enumeration of its elements between braces. For example, {2,4,6,8} represents the set consisting of the first four even natural numbers; {0,1,2,3,} is the set of all integers; {1, x , x 2, x 3,} is the set of all nonnegative powers of x ; and {1, i ,1, i } is the set of the four complex fourth roots of unity. In many cases, a set is defined by a (mathematical) statement that holds for all of its elements. Such a set is generally denoted by { x P ( x )} and read the set of all x s such that P ( x ) is true. The foregoing examples of sets can be written alternatively as follows:
In a frequently used shorthand notation, the last two sets can be abbreviated as { x n n 0 and n is an integer} and
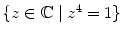
. Similarly, the unit circle can be denoted by
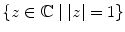
, the closed interval [ a , b ] as { x a x b }, the open interval ( a , b ) as { x a < x < b }, and the set of all nonnegative powers of x as
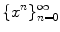
or
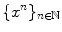
, where
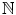
is the set of natural numbers (i.e., nonnegative integers). This last notation will be used frequently in this book. A set with a single element is called a singleton .
If a A whenever a B , we say that B is a subset of A and write B A or A B . If B A and A B , then A = B . If B A and
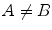
, then B is called a proper subset of A . The set defined by
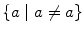
is called the empty set and is denoted by . Clearly, contains no elements and is a subset of any arbitrary set. The collection of all subsets (including ) of a set A is denoted by 2 A . The reason for this notation is that the number of subsets of a set containing n elements is 2 n when n is finite (Problem 1.1).
If A and B are sets, their union , denoted by A B , is the set containing all elements that belong to A or B or both. The intersection of the sets A and B , denoted by A B , is the set containing all elements belonging to both A and B . If { B } I is a collection of sets, we denote their union by I B and their intersection by I B .
The complement of a set A is denoted by A and defined as
The complement of B in A (or their difference) is
In any application of set theory there is an underlying universal set whose subsets are the objects of study. This universal set is usually clear from the context. For example, in the study of the properties of integers, the set of integers, denoted by
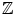
, is the universal set. The set of reals,
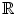
, is the universal set in real analysis, and the set of complex numbers,
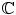
, is the universal set in complex analysis. To emphasize the presence of a universal set X , one can write X A instead of A .
From two given sets A and B , it is possible to form the Cartesian product of A and B , denoted by A B , which is the set of ordered pairs ( a , b ), where a A and b B . This is expressed in set-theoretic notation as
We can generalize this to an arbitrary number of sets. If A 1, A 2,, A n are sets, then the Cartesian product of these sets is
which is a set of ordered n -tuples. If A 1= A 2== A n = A , then we write A n instead of A A A , and
The most familiar example of a Cartesian product occurs when
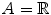
. Then
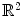
is the set of pairs ( x 1, x 2) with
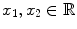
. This is simply the points in the plane. Similarly,
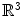
is the set of triplets ( x 1, x 2, x 3), or the points in space, and
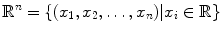
is the set of real n -tuples.
1.1.1 Equivalence Relations
There are many instances in which the elements of a set are naturally grouped together. For example, all vector potentials that differ by the gradient of a scalar function can be grouped together because they all give the same magnetic field. Similarly, all quantum state functions (of unit length) that differ by a multiplicative complex number of unit length can be grouped together because they all represent the same physical state. The abstraction of these ideas is summarized in the following definition.














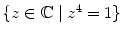 . Similarly, the unit circle can be denoted by
. Similarly, the unit circle can be denoted by 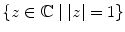 , the closed interval [ a , b ] as { x a x b }, the open interval ( a , b ) as { x a < x < b }, and the set of all nonnegative powers of x as
, the closed interval [ a , b ] as { x a x b }, the open interval ( a , b ) as { x a < x < b }, and the set of all nonnegative powers of x as 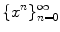 or
or 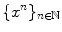 , where
, where 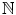 is the set of natural numbers (i.e., nonnegative integers). This last notation will be used frequently in this book. A set with a single element is called a singleton .
is the set of natural numbers (i.e., nonnegative integers). This last notation will be used frequently in this book. A set with a single element is called a singleton .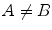 , then B is called a proper subset of A . The set defined by
, then B is called a proper subset of A . The set defined by 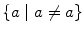 is called the empty set and is denoted by . Clearly, contains no elements and is a subset of any arbitrary set. The collection of all subsets (including ) of a set A is denoted by 2 A . The reason for this notation is that the number of subsets of a set containing n elements is 2 n when n is finite (Problem 1.1).
is called the empty set and is denoted by . Clearly, contains no elements and is a subset of any arbitrary set. The collection of all subsets (including ) of a set A is denoted by 2 A . The reason for this notation is that the number of subsets of a set containing n elements is 2 n when n is finite (Problem 1.1).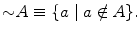
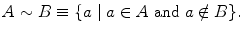
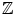 , is the universal set. The set of reals,
, is the universal set. The set of reals, 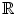 , is the universal set in real analysis, and the set of complex numbers,
, is the universal set in real analysis, and the set of complex numbers, 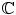 , is the universal set in complex analysis. To emphasize the presence of a universal set X , one can write X A instead of A .
, is the universal set in complex analysis. To emphasize the presence of a universal set X , one can write X A instead of A .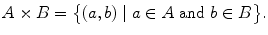
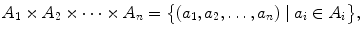
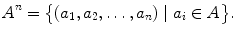
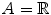 . Then
. Then 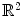 is the set of pairs ( x 1, x 2) with
is the set of pairs ( x 1, x 2) with 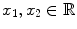 . This is simply the points in the plane. Similarly,
. This is simply the points in the plane. Similarly, 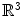 is the set of triplets ( x 1, x 2, x 3), or the points in space, and
is the set of triplets ( x 1, x 2, x 3), or the points in space, and 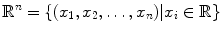 is the set of real n -tuples.
is the set of real n -tuples.