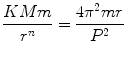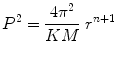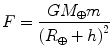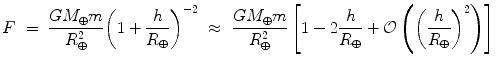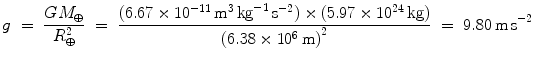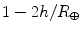A concise way to state the scientific method in astrophysics is this: We use theory to make quantitative predictions that can be compared with observations. Sometimes we can solve the relevant equations with pencil and paper in a modest number of steps, but other times we cannot. How do we proceed? Often we can use physical insight and approximate calculations to understand the salient features of a system without sweating the details. Before diving into technical material, it is good to see how physical reasoning and estimation techniques (such as toy models, scaling relations, Taylor series approximations, and dimensional analysis) offer a potent approach to astrophysics.
1.1 What Is Gravity?
Understanding gravity opens the door to studying many fascinating systems, so it is a natural place to begin. Plus, it provides a nice way to illustrate the analytic tools that infuse our inquiry. You can probably recite Newtons law of gravity,
but where does it come from? Put yourself in Isaac Newtons shoes and imagine you are trying to understand the motion of planets. Johannes Kepler has combed through reams of observational data and distilled three laws of planetary motion:
I.
Planets move in elliptical orbits, with the Sun at one focus.
II.
A line that connects a planet to the Sun sweeps out equal areas in equal times.
III.
A planets orbital period P and average distance from the Sun a are related by
These are examples of empirical laws ; they are extracted from, and provide a powerful summary of, observational data, but they do not explain in any physical way why planets move as they do. Empirical laws can, however, offer clues that help us find physical explanations, if we know how to reason with them.
The first step is to recognize that Keplers third law is an example of a scaling relation . It answers the question: If you move a planet farther from the Sun, will its orbital period increase or decrease, and by how much? The second step is to see if we can relate the scaling relation we know to something we want to learn. While I cannot say for certain, I imagine Newtons reasoning was something like this: Galileo famously demonstrated that objects of different mass fall at the same rate under the influence of gravity. Since a more massive object has more inertia, it must feel more gravity; the gravitational force should therefore be proportional to m . Then by Newtons third law of motion (equal and opposite reactions), the force must be proportional to the product Mm . Surely gravity depends on the distance between two objects; intuitively it should decrease with distance, so lets postulate
where n is unknown. Lets call the constant of proportionality K and write
The third step is to connect the two scaling relations. Here we might introduce a toy model that is deliberately simple but (we hope) rich enough to capture the essential physics. To build a toy model for motion under the influence of gravity, we ignore Keplers lesson about ellipses and just consider circles. From Newtons laws of motion, we know the force required to keep an object of mass m in a circular orbit of radius r and speed v is
where we replace the orbital speed v with the period
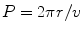
in order to connect with Kepler III. We then equate the force we have available ():
Rearranging yields
If we want to explain Keplers third law ( P 2 r 3), we apparently need the gravitational force to follow an inverse square law ( n =2). This argument is only heuristic; it cannot be taken as proof of Eq.(
Once we know the gravitational force law, we might wonder how it affects our everyday experience on Earth. Strictly speaking, we already have everything we need to determine how gravity weakens with height ( h ) above the surface of Earth (indicated by the radius R ):
This formula can be a little unwieldy, though, if we just want to know what happens when we climb a mountain or fly in an airplane. Is there any way to simplify the analysis when h is much smaller than R ? Yes! Rewriting F slightly lets us make the following approximation:
If h R then the second term in square brackets is much smaller than the first, and the third term is smaller still so we can neglect it without making a significant error. What we have done here is make a Taylor series expansion of F . This is a form of estimation that we will use from time to time when we encounter functions that are cumbersome, or we want to examine a functions behavior over some fairly narrow range. In Eq.(
The minus sign in the second term of Eq.() then says gravity weakens with height. While we knew that already, the approximation offers a simple way to quantify this effect. Suppose we ask how much gravity varies when you go up in a building or an airplane, or into the upper parts of Earths atmosphere:













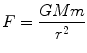
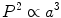
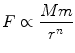
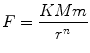
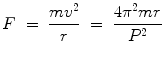
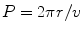 in order to connect with Kepler III. We then equate the force we have available ():
in order to connect with Kepler III. We then equate the force we have available ():