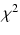1.1 Organization of the Monograph
Optical character recognition (OCR) is one of the most popular areas of research in pattern recognition []. It is a process of reading handwritten characters and recognizing them. It is widely used as a form of data entry from printed paper data records which may include passport documents, invoices, bank statements, computerized receipts, business cards, mail, printouts etc. OCR is also recognized as the subdomain of image processing which is an important research area of pattern recognition. The human brain generally finds some sort of relation predominantly in graphical form in order to remember it and recognize later. In a way it tends to produce or find patterns in handwritten characters. This led to the major motivation towards the development of OCR systems. The characters of various available languages are based on the lines and curves. An OCR can be easily designed to recognize them.
The image captured by digital camera is converted into a suitable form required by the machine. It is a common method of digitizing printed texts so that it can be electronically edited, searched, stored more compactly, displayed on-line and used in machine processes such as machine translation, text-to-speech, key data and text mining. Availability of huge datasets in several languages has created an opportunity to analyse OCR systems analytically. The major concern in these systems is the recognition accuracy. There is always an inherent degree of vagueness and impreciseness present in reallife data. Due to this recognition systems are treated here through fuzzy and rough sets encompassing indeterminate uncertainty. These uncertainty techniques form the basic mathematical foundation for different soft computing tools. A comprehensive assessment of the methods are performed through English, French, German, Latin, Hindi and Gujrati languages []. The experiments are performed on several publicly available datasets. The simulation studies reveal that the different soft computing based modeling of OCR systems performs consistently better than traditional models. The results are evaluated through different performance metrics. Several case studies are also presented on the abovementioned languages to show the benefits of soft computing models for OCR systems.
This book is written in the following divisions: (1) the introductory chapters consisting of Chaps..
The six different languages considered in this monograph are the most widely spoken language across the world. The character set used in these languages have a great degree of variation among them. Thus it would be quite unfair to place all the languages as subsections in one Chapter. This would make the situation more complex. Rather separate Chapters are devoted for the OCR system of each language where there is an opportunity for the reader to select the best soft computing based OCR system for the corresponding language. Each language in Chaps.. This will also help the reader to make a comparative analysis of each of the OCR system with respect to the six different languages considered.
Fig. 1.1
The chapter wise distribution of the OCR systems in the monograph. (OCR system 1: Fuzzy Multilayer Perceptron [])
An elementary knowledge of fuzzy and rough set theories as well as artificial neural networks [] on fuzzy sets, artificial neural networks, rough sets and genetic algorithms for better understanding.
The simulation results on the languages considered are discussed explicitly as separate sections in Chaps..
Chapters ].
1.2 Notation
It is very challenging to write a book containing appreciable amount of mathematical symbols and to achieve uniformity in the notation. Almost all the chapters of the book contain a good amount of mathematical analysis. We have tried to maintain a uniform notation within each chapter. This means that we may use the letters
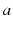
and
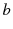
to represent a closed interval
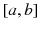
in one chapter but they could stand for parameters in a kernel function in another chapter. We have used the following uniform notation throughout the book: (1) we place tilde over a letter to denote a fuzzy or rough set
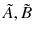
etc. and (2) all the fuzzy or rough sets are fuzzy or rough subsets of the real numbers. We use standard notations from mathematics and statistics as and when required.
The term crisp here denotes something which is neither fuzzy nor rough. A crisp set is a regular set and a crisp number is a real number. There is a potential problem with the symbol
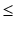
. It usually means fuzzy or rough subset as
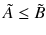
which stands for
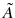
is a fuzzy or rough subset of
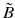
. The meaning of the symbol
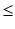
should be clear from its use. Throughout the book
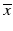
denotes mean of a random sample and not a fuzzy or rough set. It is explicitly pointed when this first arises in the book. Let
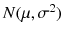
denote the normal distribution with mean
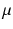
and variance
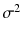
. The critical values for the normal distribution are written as
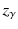
for hypothesis testing (confidence intervals). We have
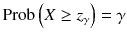
. Similarly the critical values of other distributions such as
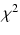












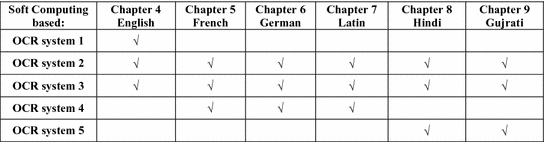
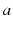 and
and  to represent a closed interval
to represent a closed interval 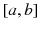 in one chapter but they could stand for parameters in a kernel function in another chapter. We have used the following uniform notation throughout the book: (1) we place tilde over a letter to denote a fuzzy or rough set
in one chapter but they could stand for parameters in a kernel function in another chapter. We have used the following uniform notation throughout the book: (1) we place tilde over a letter to denote a fuzzy or rough set 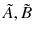 etc. and (2) all the fuzzy or rough sets are fuzzy or rough subsets of the real numbers. We use standard notations from mathematics and statistics as and when required.
etc. and (2) all the fuzzy or rough sets are fuzzy or rough subsets of the real numbers. We use standard notations from mathematics and statistics as and when required.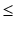 . It usually means fuzzy or rough subset as
. It usually means fuzzy or rough subset as 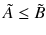 which stands for
which stands for 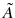 is a fuzzy or rough subset of
is a fuzzy or rough subset of 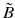 . The meaning of the symbol
. The meaning of the symbol 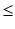 should be clear from its use. Throughout the book
should be clear from its use. Throughout the book 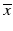 denotes mean of a random sample and not a fuzzy or rough set. It is explicitly pointed when this first arises in the book. Let
denotes mean of a random sample and not a fuzzy or rough set. It is explicitly pointed when this first arises in the book. Let 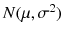 denote the normal distribution with mean
denote the normal distribution with mean 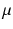 and variance
and variance 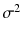 . The critical values for the normal distribution are written as
. The critical values for the normal distribution are written as 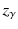 for hypothesis testing (confidence intervals). We have
for hypothesis testing (confidence intervals). We have 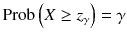 . Similarly the critical values of other distributions such as
. Similarly the critical values of other distributions such as