
 Now Available!
Now Available!  Go to
Go to
barronsbooks.com/AP/calcab/
or
barronsbooks.com/AP/calcbc/
to take a free sample
AP Calculus AB or BC test,
complete with
answer explanations and
automated scoring. *These online tests can be accessed on most mobile devices, including tablets and smartphones. About the Authors David Bock taught AP Calculus during his 35 years at Ithaca High School, and served for several years as an Exam Reader for the College Board. He also taught mathematics at Tompkins-Cortland Community College, Ithaca College, and Cornell University. A recipient of several local, state, and national teaching awards, Dave has coauthored five textbooks, and now leads workshops for AP teachers. Dennis Donovan has been a math teacher for 22 years, teaching AP Calculus for the past 19 years (8 years AB, 11 years BC).
He has served as an AP Calculus Reader and as one of nine national Question Leaders for the AP Calculus exam. Dennis leads professional development workshops for math teachers as a consultant for the College Board and a T Regional Instructor for Texas Instruments. IN MEMORIAM
Shirley O. Hockett
(1920-2013) Shirley Hockett taught mathematics for 45 years, first at Cornell University and later at Ithaca College, where she was named Professor Emerita in 1991. An outstanding teacher, she won numerous awards and authored six mathematics textbooks. Shirleys experiences as an Exam Reader and Table Leader for AP Calculus led her to write the first ever AP Calculus review book, published in 1971.
Her knowledge of calculus, attention to detail, pedagogical creativity, and dedication to students continue to shine throughout this book. On behalf of the thousands of AP Calculus students who have benefited from her tireless efforts, we gratefully dedicate this review book to Shirley. Copyright 2017, 2015, 2013, 2012, 2010, 2008 by Barrons Educational Series, Inc.
Prior editions copyright 2005, 2002, 1998 under the title How to Prepare for the AP Advanced Placement Examination in Calculus and 1995, 1992, 1987, 1983, 1971 under the title How to Prepare for the Advanced Placement Examination: Mathematics by Barrons Educational Series, Inc. All rights reserved.
No part of this work may be reproduced or distributed in any form or by any means without the written permission of the copyright owner. All inquiries should be addressed to: Barrons Educational Series, Inc. (Barrons AP Calculus Flash Cards are a great way to study these!) Understand that a derivative is an instantaneous rate of change, and be able to apply that concept to: using LHpitals rule to find limits of indeterminate forms (only 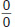 and
and 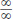 ); find equations of tangent lines; determine where a function is increasing/decreasing, concave up/down, or has maxima, minima, or points of inflection; analyze the speed, velocity, and acceleration of an object in motion; solve related rates problems, using implicit differentiation when necessary. (Barrons AP Calculus Flash Cards are a great way to study these!) Understand that a derivative is an instantaneous rate of change, and be able to apply that concept to: using LHpitals rule to find limits of indeterminate forms (only
); find equations of tangent lines; determine where a function is increasing/decreasing, concave up/down, or has maxima, minima, or points of inflection; analyze the speed, velocity, and acceleration of an object in motion; solve related rates problems, using implicit differentiation when necessary. (Barrons AP Calculus Flash Cards are a great way to study these!) Understand that a derivative is an instantaneous rate of change, and be able to apply that concept to: using LHpitals rule to find limits of indeterminate forms (only 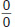 and
and 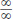 ); find equations of tangent lines; determine where a function is increasing/decreasing, concave up/down, or has maxima, minima, or points of inflection; analyze the speed, velocity, and acceleration of an object in motion; solve related rates problems, using implicit differentiation when necessary.
); find equations of tangent lines; determine where a function is increasing/decreasing, concave up/down, or has maxima, minima, or points of inflection; analyze the speed, velocity, and acceleration of an object in motion; solve related rates problems, using implicit differentiation when necessary.
Understand that integrals represent accumulation functions based on antiderivatives, and be able to apply those concepts to: the average value of a function; area and volume; position of object in motion and distance traveled; total amount when given the rate of accumulation; differential equations, including solutions and slope fields. Be able to apply any of the above calculus concepts to functions defined algebraically, graphically, or in tables. Be able to maximize your score on the exam by: answering all the multiple-choice questions; knowing how and when to use your calculator, and when not to; understanding what work you need to show; knowing how to explain, interpret, and justify answers when a question requires that. (The free-response solutions in this book model such answers.) Barrons Essential As you review the content in this book to work toward earning that on your AP CALCULUS BC exam, here are five things that you MUST know above everything else: Master the Essential 5 listed for the AB Calculus Exam. These form the core for questions that determine your AB subscore, and provide the essential knowledge base youll need for questions related to the additional BC topics. Understand how to extend AB Calculus concepts to more advanced situations, including: using limits to analyze improper integrals; solving logistic differential equations and estimating solutions using Eulers method; finding antiderivatives using integration by parts or partial fractions; finding arc lengths.
Be able to apply calculus concepts to parametrically defined functions and polar functions. Know how to analyze the position, velocity, speed, acceleration, and distance traveled for an object in motion in two dimensions by applying calculus concepts to vectors. Understand infinite series. You must be able to: determine whether a series converges or diverges; use Taylors theorem to represent functions as power series; determine the interval of convergence for a power series; find bounds on the error for estimates based on series. Welcome to Barrons AP Calculus AB and BC eBook! All equations, tables, graphs, and other illustrations may appear differently depending on what you are using to view it on, please adjust your setting preferences accordingly. This book contains hundreds of hyperlinks that will help you navigate through its content, bring you to helpful resources, and allow you to click between all questions and answers.
Good luck!  T his book is intended for students who are preparing to take either of the two Advanced Placement Examinations in Mathematics offered by the College Entrance Examination Board, and for their teachers. It is based on the May 2014 course description published by the College Board, and covers the topics listed there for both Calculus AB and Calculus BC. Candidates who are planning to take the CLEP Examination on Calculus with Elementary Functions are referred to the section of this Introduction on that examination. Calculus AB and BC are both full-year courses in the calculus of functions of a single variable. Both courses emphasize: (1) student understanding of concepts and applications of calculus over manipulation and memorization; (2) developing the students ability to express functions, concepts, problems, and conclusions analytically, graphically, numerically, and verbally, and to understand how these are related; and (3) using a graphing calculator as a tool for mathematical investigations and for problem-solving. Both courses are intended for those students who have already studied college-preparatory mathematics: algebra, geometry, trigonometry, analytic geometry, and elementary functions (linear, polynomial, rational, exponential, logarithmic, trigonometric, inverse trigonometric, and piecewise).
T his book is intended for students who are preparing to take either of the two Advanced Placement Examinations in Mathematics offered by the College Entrance Examination Board, and for their teachers. It is based on the May 2014 course description published by the College Board, and covers the topics listed there for both Calculus AB and Calculus BC. Candidates who are planning to take the CLEP Examination on Calculus with Elementary Functions are referred to the section of this Introduction on that examination. Calculus AB and BC are both full-year courses in the calculus of functions of a single variable. Both courses emphasize: (1) student understanding of concepts and applications of calculus over manipulation and memorization; (2) developing the students ability to express functions, concepts, problems, and conclusions analytically, graphically, numerically, and verbally, and to understand how these are related; and (3) using a graphing calculator as a tool for mathematical investigations and for problem-solving. Both courses are intended for those students who have already studied college-preparatory mathematics: algebra, geometry, trigonometry, analytic geometry, and elementary functions (linear, polynomial, rational, exponential, logarithmic, trigonometric, inverse trigonometric, and piecewise).
Next page








 Now Available!
Now Available!  Go to
Go to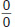 and
and 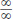 ); find equations of tangent lines; determine where a function is increasing/decreasing, concave up/down, or has maxima, minima, or points of inflection; analyze the speed, velocity, and acceleration of an object in motion; solve related rates problems, using implicit differentiation when necessary. (Barrons AP Calculus Flash Cards are a great way to study these!) Understand that a derivative is an instantaneous rate of change, and be able to apply that concept to: using LHpitals rule to find limits of indeterminate forms (only
); find equations of tangent lines; determine where a function is increasing/decreasing, concave up/down, or has maxima, minima, or points of inflection; analyze the speed, velocity, and acceleration of an object in motion; solve related rates problems, using implicit differentiation when necessary. (Barrons AP Calculus Flash Cards are a great way to study these!) Understand that a derivative is an instantaneous rate of change, and be able to apply that concept to: using LHpitals rule to find limits of indeterminate forms (only  T his book is intended for students who are preparing to take either of the two Advanced Placement Examinations in Mathematics offered by the College Entrance Examination Board, and for their teachers. It is based on the May 2014 course description published by the College Board, and covers the topics listed there for both Calculus AB and Calculus BC. Candidates who are planning to take the CLEP Examination on Calculus with Elementary Functions are referred to the section of this Introduction on that examination. Calculus AB and BC are both full-year courses in the calculus of functions of a single variable. Both courses emphasize: (1) student understanding of concepts and applications of calculus over manipulation and memorization; (2) developing the students ability to express functions, concepts, problems, and conclusions analytically, graphically, numerically, and verbally, and to understand how these are related; and (3) using a graphing calculator as a tool for mathematical investigations and for problem-solving. Both courses are intended for those students who have already studied college-preparatory mathematics: algebra, geometry, trigonometry, analytic geometry, and elementary functions (linear, polynomial, rational, exponential, logarithmic, trigonometric, inverse trigonometric, and piecewise).
T his book is intended for students who are preparing to take either of the two Advanced Placement Examinations in Mathematics offered by the College Entrance Examination Board, and for their teachers. It is based on the May 2014 course description published by the College Board, and covers the topics listed there for both Calculus AB and Calculus BC. Candidates who are planning to take the CLEP Examination on Calculus with Elementary Functions are referred to the section of this Introduction on that examination. Calculus AB and BC are both full-year courses in the calculus of functions of a single variable. Both courses emphasize: (1) student understanding of concepts and applications of calculus over manipulation and memorization; (2) developing the students ability to express functions, concepts, problems, and conclusions analytically, graphically, numerically, and verbally, and to understand how these are related; and (3) using a graphing calculator as a tool for mathematical investigations and for problem-solving. Both courses are intended for those students who have already studied college-preparatory mathematics: algebra, geometry, trigonometry, analytic geometry, and elementary functions (linear, polynomial, rational, exponential, logarithmic, trigonometric, inverse trigonometric, and piecewise).