TheBanachTarskiParadoxisamoststrikingmathematicalconstruction:itassertsthatasolidballcanbetakenapartintofinitelymanypiecesthatcanberearrangedusingrigidmotionstoformaballtwiceaslarge.Thisvolumeexplorestheconsequencesoftheparadoxformeasuretheoryanditsconnectionswithgrouptheory,geometry,settheory,andlogic.
Thisneweditionofaclassicbookunifiescontemporaryresearchontheparadox.Ithasbeenupdatedwithmanynewproofsandresultsanddiscussionsofthemanyproblemsthatremainunsolved.Amongthenewresultspresentedareseveralunusualparadoxesinthehyperbolicplane,oneofwhichinvolvestheshapesofEschersfamousAngelandDevilswoodcut.Anewchapterisdevotedtoacompleteproofoftheremarkableresultthatthecirclecanbesquaredusingsettheory,aproblemthathadbeenopenforoversixtyyears.
GrzegorzTomkowicz isaself-educatedPolishmathematicianwhohasmadeseveralimportantcontributionstothetheoryofparadoxicaldecompositionsandinvariantmeasures.
StanWagon isaProfessorofMathematicsatMacalesterCollege.HeisawinneroftheWolframResearchInnovatorAward,aswellasnumerouswritingawardsincludingtheFord,Evans,andtheAllendoerferAwards.Hispreviousworkincludes ACourseinComputationalNumberTheory (2000), TheSIAM100-DigitChallenge (2004)and MathematicainAction (3rdEd.2010).
EncyclopediaofMathematicsanditsApplications
Thisseriesisdevotedtosignificanttopicsorthemesthathavewideapplicationinmathematicsormathematicalscienceandforwhichadetaileddevelopmentoftheabstracttheoryislessimportantthanathoroughandconcreteexplorationoftheimplicationsandapplications.
Booksinthe EncyclopediaofMathematicsanditsApplications covertheirsubjectscomprehensively.Lessimportantresultsmaybesummarizedasexercisesattheendsofchapters.Fortechnicalities,readerscanbereferredtothebibliography,whichisexpectedtobecomprehensive.Asaresult,volumesareencyclopedicreferencesormanageableguidestomajorsubjects.
Encyclopedia of Mathematics and its Applications
All the titles listed below can be obtained from good booksellers or from Cambridge University Press. For a complete series listing visit
www.cambridge.org/mathematics.
The BanachTarski Paradox
Second Edition
Grzegorz Tomkowicz
Centrum Edukacji G2, Bytom, Poland
Stan Wagon
Macalester College, St. Paul, Minnesota

One Liberty Plaza, New York, NY 10006
Cambridge University Press is part of the University of Cambridge.
It furthers the Universitys mission by disseminating knowledge in the pursuit of education, learning, and research at the highest international levels of excellence.
www.cambridge.org
Information on this title: www.cambridge.org/9781107042599
Cambridge University Press 2016
This publication is in copyright. Subject to statutory exception and to the provisions of relevant collective licensing agreements, no reproduction of any part may take place without the written permission of Cambridge University Press.
First published 2016
Printed in the United States of America
A catalog record for this publication is available from the British Library.
Library of Congress Cataloging in Publication Data
Names: Tomkowicz, Grzegorz. | Wagon, S.
Title: The Banach-Tarski paradox.
Description: Second edition / Grzegorz Tomkowicz, Centrum Edukacji G2, Bytom,
Poland, Stan Wagon, Macalester College, St. Paul, Minnesota. | New York,
NY : Cambridge University Press, [2016] | Series: Encyclopedia of
mathematics and its applications ; 163 | Previous edition: The
Banach-Tarski paradox / Stan Wagon (Cambridge : Cambridge University
Press, 1985). | Includes bibliographical references and index.
Identifiers: LCCN 2015046410 | ISBN 9781107042599 (hardback : alk. paper)
Subjects: LCSH: Banach-Tarski paradox. | Measure theory. | Decomposition
(Mathematics)
Classification: LCC QA248 .W22 2016 | DDC 511.3/22dc23
LC record available at http://lccn.loc.gov/2015046410
ISBN 978-1-107-04259-9 Hardback
Cambridge University Press has no responsibility for the persistence or accuracy of URLs for external or third-party Internet Web sites referred to in this publication and does not guarantee that any content on such Web sites is, or will remain, accurate or appropriate.
To Jan Mycielski, whose enthusiasm and
knowledge strongly influenced both of us
DELIANS: How can we be rid of the plague?
DELPHIC ORACLE: Construct a cubic altar having double the size of the existing one.
BANACH AND TARSKI: Can we use the Axiom of Choice?
Contents
Jan Mycielski
Part One
1.1
1.2
4.1
4.2
4.3
4.4
4.5
4.6
5.1
5.2
5.3
6.1
6.2
6.3
7.1
7.2
7.3
8.1
8.2
9.1
9.2
9.3
10.1
10.2
10.3
Part Two
11.1
11.2
11.3
12.1
12.2
12.3
12.4
12.5
13.1
13.2
13.3
13.4
13.5
14.1
14.2
14.3
14.4
15.1
15.2
15.3
A
B
C
Foreword
This book is motivated by the following theorem of Hausdorff, Banach, andTarski: Given any two bounded sets 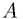 and
and 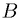 in three-dimensional space
in three-dimensional space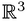 , each having nonempty interior, one can partition
, each having nonempty interior, one can partition 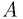 into finitely manydisjoint parts and rearrange them by rigid motions to form
into finitely manydisjoint parts and rearrange them by rigid motions to form 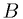 . This, I believe,is the most surprising result of theoretical mathematics. It shows the imaginarycharacter of the unrestricted idea of a set in
. This, I believe,is the most surprising result of theoretical mathematics. It shows the imaginarycharacter of the unrestricted idea of a set in 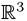 . It precludes the existence offinitely additive, congruence-invariant measures over all bounded subsets of
. It precludes the existence offinitely additive, congruence-invariant measures over all bounded subsets of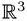 , and it shows the necessity of more restricted constructions, such asLebesgue measure.
, and it shows the necessity of more restricted constructions, such asLebesgue measure.
In the 1950s, the years of my mathematical education in Poland, this resultwas often discussed. J. F. Adams, T. J. Dekker, J. von Neumann, R. M.Robinson, and W. Sierpiski wrote about it; my PhD thesis was motivated byit. (All this is referenced in this book.) Thus it is a great pleasure to introduceyou to this book, where this striking theorem and many related results ingeometry and measure theory, and the underlying tools of group theory, arepresented with care and enthusiasm. The reader will also find someapplications of the most recent advances of group theory to measuretheory: the work of Gromov, Margulis, Rosenblatt, Sullivan, Tits, andothers.
















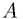 and
and 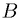 in three-dimensional space
in three-dimensional space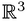 , each having nonempty interior, one can partition
, each having nonempty interior, one can partition 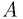 into finitely manydisjoint parts and rearrange them by rigid motions to form
into finitely manydisjoint parts and rearrange them by rigid motions to form 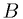 . This, I believe,is the most surprising result of theoretical mathematics. It shows the imaginarycharacter of the unrestricted idea of a set in
. This, I believe,is the most surprising result of theoretical mathematics. It shows the imaginarycharacter of the unrestricted idea of a set in 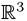 . It precludes the existence offinitely additive, congruence-invariant measures over all bounded subsets of
. It precludes the existence offinitely additive, congruence-invariant measures over all bounded subsets of , and it shows the necessity of more restricted constructions, such asLebesgue measure.
, and it shows the necessity of more restricted constructions, such asLebesgue measure.