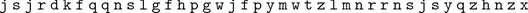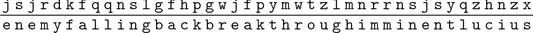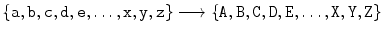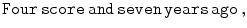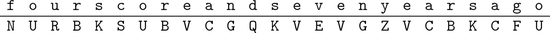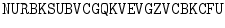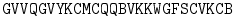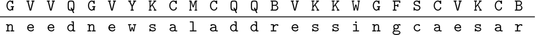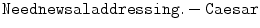Jeffrey Hoffstein Jill Pipher - An Introduction to Mathematical Cryptography

An Introduction to Mathematical Cryptography — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "An Introduction to Mathematical Cryptography" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

1234567...240

Springer Science+Business Media New York 2014

Jeffrey Hoffstein , Jill Pipher and Joseph H. Silverman An Introduction to Mathematical Cryptography Undergraduate Texts in Mathematics 10.1007/978-1-4939-1711-2_1

1. An Introduction to Cryptography

Jeffrey Hoffstein 1, Jill Pipher 1 and Joseph H. Silverman 1

(1)

Department of Mathematics, Brown University, Providence, RI, USA

1.1 Simple Substitution Ciphers

As Julius Caesar surveys the unfolding battle from his hilltop outpost, an exhausted and disheveled courier bursts into his presence and hands him a sheet of parchment containing gibberish:

Within moments, Julius sends an order for a reserve unit of charioteers to speed around the left flank and exploit a momentary gap in the opponents formation.

How did this string of seemingly random letters convey such important information? The trick is easy, once it is explained. Simply take each letter in the message and shift it five letters up the alphabet. Thus j in the ciphertext becomes e in the plaintext , because e is followed in the alphabet by f , g , h , i , j . Applying this procedure to the entire ciphertext yields

The second line is the decrypted plaintext, and breaking it into words and supplying the appropriate punctuation, Julius reads the message

Enemy falling back. Breakthrough imminent. Lucius.

There remains one minor quirk that must be addressed. What happens when Julius finds a letter such as d ? There is no letter appearing five letters before d in the alphabet. The answer is that he must wrap around to the end of the alphabet. Thus d is replaced by y , since y is followed by z , a , b , c , d .

This wrap-around effect may be conveniently visualized by placing the alphabet abcdxyz around a circle, rather than in a line. If a second alphabet circle is then placed within the first circle and the inner circle is rotated five letters, as illustrated in Fig.

Although the details of the preceding scene are entirely fictional, and in any case it is unlikely that a message to a Roman general would have been written in modern English(!), there is evidence that Caesar employed this early method of cryptography, which is sometimes called the Caesar cipher in his honor. It is also sometimes referred to as a shift cipher , since each letter in the alphabet is shifted up or down. Cryptography , the methodology of concealing the content of messages, comes from the Greek root words kryptos , meaning hidden, and graphikos , meaning writing. The modern scientific study of cryptography is sometimes referred to as cryptology .

Figure 1.1:

A cipher wheel with an offset of five letters

In the Caesar cipher, each letter is replaced by one specific substitute letter. However, if Bob encrypts a message for Alice using a Caesar cipher and allows the encrypted message to fall into Eves hands, it will take Eve very little time to decrypt it. All she needs to do is try each of the 26 possible shifts.

Bob can make his message harder to attack by using a more complicated replacement scheme. For example, he could replace every occurrence of a by z and every occurrence of z by a , every occurrence of b by y and every occurrence of y by b , and so on, exchanging each pair of letters c x ,, m n .

This is an example of a simple substitution cipher , that is, a cipher in which each letter is replaced by another letter (or some other type of symbol). The Caesar cipher is an example of a simple substitution cipher, but there are many simple substitution ciphers other than the Caesar cipher. In fact, a simple substitution cipher may be viewed as a rule or function

assigning each plaintext letter in the domain a different ciphertext letter in the range. (To make it easier to distinguish the plaintext from the ciphertext, we write the plaintext using lowercase letters and the ciphertext using uppercase letters.) Note that in order for decryption to work, the encryption function must have the property that no two plaintext letters go to the same ciphertext letter. A function with this property is said to be one-to-one or injective .

A convenient way to describe the encryption function is to create a table by writing the plaintext alphabet in the top row and putting each ciphertext letter below the corresponding plaintext letter.

Example 1.1.

A simple substitution encryption table is given in Table . The ciphertext alphabet (the uppercase letters in the bottom row) is a randomly chosen permutation of the 26 letters in the alphabet. In order to encrypt the plaintext message

we run the words together, look up each plaintext letter in the encryption table, and write the corresponding ciphertext letter below.

It is then customary to write the ciphertext in five-letter blocks:

Table 1.1:

Simple substitution encryption table

Decryption is a similar process. Suppose that we receive the message

and that we know that it was encrypted using Table . Using this table, we easily decrypt the message.

Putting in the appropriate word breaks and some punctuation reveals an urgent request!

Table 1.2:

Simple substitution decryption table

1.1.1 Cryptanalysis of Simple Substitution Ciphers

How many different simple substitution ciphers exist? We can count them by enumerating the possible ciphertext values for each plaintext letter. First we assign the plaintext letter a to one of the 26 possible ciphertext letters A Z . So there are 26 possibilities for a . Next, since we are not allowed to assign b to the same letter as a , we may assign b to any one of the remaining 25 ciphertext letters. So there are 26 25=650 possible ways to assign a and b . We have now used up two of the ciphertext letters, so we may assign c to any one of the remaining 24 ciphertext letters. And so on. Thus the total number of ways to assign the 26 plaintext letters to the 26 ciphertext letters, using each ciphertext letter only once, is

Next page

1234567...240

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

Similar books «An Introduction to Mathematical Cryptography»

Look at similar books to An Introduction to Mathematical Cryptography. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.

Mary Pipher

The Middle of Everywhere: The Worlds Refugees Come to Our Town

Mary Pipher

The Shelter of Each Other

Khaled Salah Mohamed

New Frontiers in Cryptography: Quantum, Blockchain, Lightweight, Chaotic and DNA

Wade Trappe

Introduction to Cryptography: With Coding Theory

Phillip Bonacich and Philip Lu

Introduction to Mathematical Sociology

Jean-Philippe Aumasson

Serious Cryptography: A Practical Introduction to Modern Encryption

Murphy Sean

Cryptography: A Very Short Introduction

Jeffrey James Stapleton

Security Without Obscurity: A Guide to Cryptographic Architectures

Jeffrey S. Saltz

An Introduction to Data Science

JEFFREY A. STRAKOWSKI

Introduction to Musculoskeletal Ultrasound: Getting Started

Keith M. Martin

Everyday cryptography: Fundamental principles and applications

Lawrence C. Washington

Elliptic Curves: Number Theory and Cryptography

Discussion, reviews of the book An Introduction to Mathematical Cryptography and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.