Stewart - Professor Stewarts cabinet of mathematical curiosities

Professor Stewarts cabinet of mathematical curiosities — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Professor Stewarts cabinet of mathematical curiosities" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

1234567...70

Acknowledgements

The following figures are reproduced with the permission of the named copyright holders:

Pages 30, 280 (What Seamus Didnt Know); Suppiya Siranan.

Page 41 (What is the Area of an Ostrich Egg?); Hierakonpolis expedition, leader Rene Friedman, photograph by James Rossiter.

Page 69 (Mathematical Cats); Dr Sergey P. Kuznetsov, Laboratory of Theoretical Nonlinear Dynamics, SB IRE RAS.

Page 92 (How to See Inside Things); Brad Petersen.

Page 107 (Alexanders Horned Sphere); from Topology by John G. Hocking and Gail S. Young, Addison-Wesley, 1961.

Page 113 (Just a Phase Im Going Through); GNU Free Documentation License, Free Software Foundation (www.gnu.org/copyleft/fdl.html).

Page 182 (The Klein Bottle); Janet Chao (www.illustrationideas.com).

Page 184 (The Klein Bottle); Konrad Polthier, Free University of Berlin.

Page 190 (Multiplying with Sticks); Eric Marcotte PhD (www.sliderule.ca).

Page 216 (How to Turn a Sphere Inside Out); Bruce Puckett.

By the Same Author

Concepts of Modern Mathematics
Game, Set, and Math
Does God Play Dice?
Another Fine Math Youve Got Me Into
Fearful Symmetry (with Martin Golubitsky)
Natures Numbers
From Here to Infinity
The Magical Maze
Lifes Other Secret
Flatterland
What Shape Is a Snowflake?
The Annotated Flatland (with Edwin A. Abbott)
Math Hysteria
The Mayor of Uglyvilles Dilemma
Letters to a Young Mathematician
How to Cut a Cake
Why Beauty Is Truth
Taming the Infinite
Professor Stewarts Cabinet of Mathematical Curiosities

with Jack Cohen
The Collapse of Chaos
Figments of Reality
What Does a Martian Look Like?
Wheelers (science fiction)
Heaven (science fiction)

with Terry Pratchett and Jack Cohen
The Science of Discworld
The Science of Discworld II: The Globe
The Science of Discworld III: Darwins Watch

Professor Stewarts Superlative Storehouse of Sneaky Solutions and Stimulating Supplements

Wherein the perspicacious or perplexed reader may procure answers to those questions that are presently known to possess answers ... together with such gratuitous facts and fancies as may facilitate their further delectation and enlightenment.

Calculator Curiosity 1

(88) + 13 = 77
(888) + 13 = 717
(8888) + 13 = 7117
(88888) + 13 = 71117
(888888) + 13 = 711117
(8888888) + 13 = 7111117
(88888888) + 13 = 71111117
(888888888) + 13 = 711111117

Year Turned Upside Down

Past: 1961; Future: 6009.

If you insist on allowing a squiggle on the 7, amend these to 2007 and 2117.

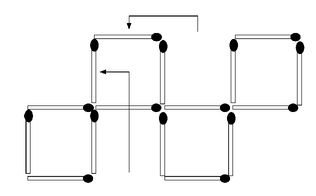
Sixteen Matches

Move these two.

Swallowing Elephants

The deduction is false.

Suppose, for the sake of argument, that elephants are easy to swallow. Then the third statement in the puzzle tells us that elephants eat honey. The second then tells us that elephants can play the bagpipes. On the other hand, the first statement tells us that elephants wear pink trousers, in which case the fourth statement tells us that elephants cant play the bagpipes. So we get a logical contradiction. The only way out is if elephants are not easy to swallow.

Theres a systematic method for answering such questions. First, turn everything into symbols. Let

E be the statement: Is an elephant.
H be the statement: Eats honey.
S be the statement: Is easy to swallow.
P be the statement: Wears pink trousers.
B be the statement: Can play the bagpipes.

We use the logical symbols

meaning implies
meaning not.

Then the first four statements read:

E P
H B
S H
P B

We need two of the mathematical laws of logic:

X Y is the same as Y X
If X Y Z, then X Z

Using these, we can rewrite the conditions as:

E P B H S

so E S. That is, elephants are not easy to swallow.

This list of attributes suggests yet another way to get the answer: think about an elephant (E) that (P) wears pink trousers, ( B) does not play the bagpipes, ( H) does not eat honey, and ( S) is not easy to swallow. Then all four statemnts in the puzzle are true, but elephants are easy to swallow is false.

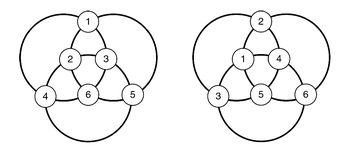
Magic Circle

These or their rotations and reflections.

Press-the-Digit-ation

The explanation of Whodunnis calculator trick uses a bit of algebra.

Suppose you live in house number x, were born in year y, and have had z birthdays so far this year, which is either 0 or 1, depending on dates. Then successive steps in the trick go like this:

Enter your house number: x

Double it: 2x

Add 42: 2x + 42

Multiply by 50: 50(2x + 42) = 100x + 2100

Subtract the year of your birth: 100x + 2100 - y

Subtract 50: 100x + 2050 - y

Add the number of birthdays you have had this year: 100x + 2050 - y + z

Subtract 42: 100x + 2008 - y + z

If were doing the trick in 2009, then 2008 - y is one less than the number of years that have passed since your birth year. Adding the number of birthdays youve had this year leaves it that way if you havent had one yet, but adds 1 if you have. The result is always your age. (Think about it. If you were born one year ago but havent had a birthday yet, your age is 0. After your birthday, its 1.)

So the final result is 100x + your age. So provided you are aged between 1 and 99, the last two digits will be your age (written as 01- 09 if your age is 1-9). Removing those and dividing by 100, which is the same as looking at the remaining digits, gives x - your house number.

If youre over 99, then the final two digits cant be your age. There will be an extra digit (which barring medical miracles will be 1). So your age will be 1 followed by the final two digits. And your house number will be the rest of the digits except those two, minus one.

If youre age 0, the trick still works provided you count the day of your birth as a birth-day. Your zeroth, in fact. But usually we dont do that, which is why I excluded age 0.

To modify the trick for any other year, say 2009 + a, just change the final step to subtract 42 - a. So in 2010 subtract 41, in 2011 subtract 40, and so on. If youre reading this after 2051, make that add a - 42. Its the same thing, but it will sound more sensible.

Secrets of the Abacus

To subtract (say) a 3-digit number [x][y][z], which is really 100x + 10y + z, we have to form the complement [10 - x][10 - y] [10 - z], which is really 100(10 - x) + 10(10 - y) + (10 - z). This is equal to 1000 - 100x + 100 - 10y + 10 - z, or 1110 - (100x + 10y + z). So adding the complement is the same as subtracting the original number, but adding 1110. To get rid of it, subtract 1 from positions 4, 3, 2, but not 1.

Redbeards Treasure

Redbeard will locate the lost loot 128 paces north of the rock.

At each step the piratical finger can move either left or right - two choices. So the number of routes down the diagram doubles for each extra row. There are 8 rows, and only one T to start from, so the number of routes is 12222222 = 128.

Next page

1234567...70

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

Similar books «Professor Stewarts cabinet of mathematical curiosities»

Look at similar books to Professor Stewarts cabinet of mathematical curiosities. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.

Norvin Pallas

Calculator Puzzles, Tricks and Games

Jerome S. Meyer

Puzzles, Games, & Tricks: Understanding the Mystery and Magic of Numbers

Jason Rosenhouse

Games for Your Mind: The History and Future of Logic Puzzles

Shasha

Dr. Eccos cyberpuzzles: 36 puzzles for hackers and other mathematical detectives

Kordemsky

The Moscow Puzzles: 359 Mathematical Recreations

Gianni A. Sarcone

Impossible Folding Puzzles and Other Mathematical Paradoxes

Barry R. Clarke

Mathematical Puzzles and Curiosities

Ian Stewart

Professor Stewart’s Cabinet of Mathematical Curiosities

Ian Stewart

How to Cut a Cake: And Other Mathematical Conundrums

Oswald Jacoby

Intriguing Mathematical Problems

Owen O’Shea

The Call of the Primes: Surprising Patterns, Peculiar Puzzles, and Other Marvels of Mathematics

Ian Stewart

Professor Stewart’s Casebook of Mathematical Mysteries

Discussion, reviews of the book Professor Stewarts cabinet of mathematical curiosities and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.