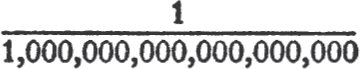Jerome S. Meyer - Puzzles, Games, & Tricks: Understanding the Mystery and Magic of Numbers

First published in 1961 as Fun with Mathematics by Premier Books, Fawcett Publications, Inc., Greenwich, Connecticut

First Skyhorse Publishing Edition 2017

All rights to any and all materials in copyright owned by the publisher are strictly reserved by the publisher.

Skyhorse Publishing books may be purchased in bulk at special discounts for sales promotion, corporate gifts, fund-raising, or educational purposes. Special editions can also be created to specifications. For details, contact the Special Sales Department, Skyhorse Publishing, 307 West 36th Street, 11th Floor, New York, NY 10018 or .

Skyhorse and Skyhorse Publishing are registered trademarks of Skyhorse Publishing, Inc., a Delaware corporation.

Visit our website at www.skyhorsepublishing.com.

10 9 8 7 6 5 4 3 2 1

Library of Congress Cataloging-in-Publication Data is available on file.

Cover artwork: iStockphoto

Print ISBN: 978-1-5107-2780-9

Ebook ISBN: 978-1-5107-2781-6

Printed in the United States of America

To
All Young People
Who Love Mathematics

CONTENTS

PREFACE

IN writing Fun with Mathematics I have tried to include a great deal of new material that would interest everyone for whom mathematics has an appeal. The section on More and More of Less and Less gives in everyday common experience the fundamental principles of differential and integral calculus. The section on , i and e explains the mystery and fascination of the imaginary numbers, and gives the derivation and application of logarithms in language that any freshman in high school can readily understand. As far as I know, the method of making a good slide rule from an ordinary ruler has never been published before, nor has the chart ever appeared in a book which instantly solves problems of the right triangle without the necessity of knowing any trigonometry. In the section on Mathematical How-to-dos you will learn how to divide a circle into any number of equal parts, how to enlarge or reduce a picture, how to make a sundial and shadow stick that will tell the time and date anywhere, and many other how-to-dos.

You dont need a knowledge of mathematics to enjoy this book, but if you have a smattering of elementary mathematics you will enjoy it all the more. Of special interest to the trickster is the section by Royal Heath on magic squares that work upside down and in the mirror as well as right side up. Here you will find many tricks and stunts based on mathematical principles.

In conclusion I want to thank Dr. Jekuthiel Ginsburg of Yeshiva University for permission to reprint some of the curiosa which appeared in Scripta Mathematica; Mr. Aaron Bakst for permission to use his method of deriving logarithms quickly as given in his book Mathematics, Its Magic and Mastery (published by Van Nostrand); to E. P. Dutton and Company, Crown Publishers and Greenberg: Publisher for permission to reprint some of the problems in my books Fun-to-Do, Puzzle Paradise , and Fun for the Family; and to Royal V. Heath for his fascinating section on The Magic of Numbers. My sincere thanks also to Dr. John Storck and Stephen W. Leibholz for their valuable assistance in editing and correcting this book.

JEROME S. MEYER

THE WORLD OF NUMBERS

EXPLORING BOTH ENDS OF OUR NUMBER SYSTEM

WE ORDINARY mortals live in a world of numbers just about halfway between the inconceivably large and the incredibly small. The numbers in our lives range between several million in the upper limit to about 1/10000 in the lower limit, and in the daily personal lives of most of us numbers greater than a few thousand or smaller than a sixteenth of an inch seldom appear.

When numbers get into the hundreds of millions or billions they have no meaning for us. We read of the population of the United States being 150,000,000 but cant possibly conceive such a large number, and numbers like the money for defense or the total national debtrunning into the hundreds of billions-make us yawn and say Well, well. Of course if you are a banker or the owner of a high-circulation magazine, numbers in the millions dont faze you; if you are a highly skilled mechanic working in an airplane factory a ten-thousandth of an inch reading on a micrometer is nothing unusual. But who ever hears of a trillion or quadrillion or sextillion or an octo-vigintillionth of a gram in ordinary conversation? These terms, outlandish and impractical as they seem to us, belong to the scientist who not only eats them for breakfast but uses them to produce the thousands of scientific miracles that make our lives comfortable and our living standards the highest in the world.

To the astronomer a number like 5,000,000,000,000,000,000 miles is all in a days work. It represents the distance in miles of a certain nebula or star cluster from the earth. It is 5 quintillion miles or somewhat less than one million light years. A light year is the distance that light, traveling at 186,000 miles per second, will travel in a year. To the atomic physicist a single gram contains about 1,000,000,000,000,000,000,000,000,000 electrons. This is more electrons than there are drops of water in the Atlantic and Pacific Oceans combined! Yes, unlike you and me, these scientists live in a world of numbers far beyond our comprehension, and they are continually playing with the very great or the very small.

Of course they dont write these giants or pigmies out in ciphers: that would be a waste of time and space. They merely represent them in powers of 10. The exponent tells the number of ciphers, so when you see 1024 you know that it means 1 with 24 zeroes after the 1. When you see 1018 you know that it is a fraction with 1 in the numerator and 1 followed by 18 zeros in the denominator:

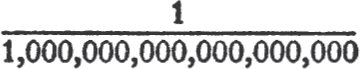
When the physicist speaks of the mass of the earth being 5.9 1027 grams he saves himself from writing 5,900,000,000,000,000,000,000,000,000 grams. When he tells us that the energy locked up in a pound of matter is 4 1023 ergs he cant be bothered to write 400,000,000,000,000,000,000,000. We shall meet numbers in this section that are of this amazingly large or small order, so we might as well get used to the mathematical way of writing them.

NUMBER GIANTSHOW MUCH IS A BILLION?

SUPPOSE YOU had a billion dollars and, in your desire to be entirely unique, you decided to invest it, without interest or dividends, in a very bad stock company. Now suppose the corporation was so poorly run that it succeeded in losing a thousand dollars of your money every day in the week and still managed to stay in business. It would take more than two thousand years for you to lose that billion dollars!

Again assuming that you are seventeen years old and started now to count up to a billion, one count every second, day and night without stopping to eat or sleep. Of course you couldnt do this without going on shifts, so well assume that two of your seventeen-year-old friends help you out. By the time you reached a billion you would be in your late forties.

If your fountain pen were enlarged one billion times it would be 95,000 miles long and 8,000 miles high. The cap of your pen would be big enough to enclose the earth, whose diameter is roughly 7,900 miles. But a billion is only 109 and that is a mere nothing compared to the real giants. Suppose it were possible to tear a sheet of paper of a certain size and of about the thickness of this page, in half; and then to tear the pieces again in half, and then again in half, and to keep this up for fifty tearings. Each time you would be doubling the number of sheets of paper. The question is: How high a pile would fifty tearings make, and how big a sheet would you need to begin with, to get final sheets of about the size of this page? The answer is incredible but it can be easily verified. It is 2 raised to the 50th power and turns out to be 1,125,899,906,842,624 sheets of paper. Since each sheet would measure about one third of a square foot, this comes to 375,299,968,947,541 square feet or over 13,000,000 square miles, or a little less than one quarter the land area of the entire earth. Figuring 400 of these sheets to the inch, we would have a pile about 2,860,000,000,000 inches high. Divide this by 12 and we get about 230,000,000,000 feet. Now one million feet come to approximately 190 miles, so the pile would be more than 38,000,000 miles high!