Philip Carter - The Complete Book of Fun Maths: 250 Confidence-boosting Tricks, Tests and Puzzles

The Complete Book of Fun Maths: 250 Confidence-boosting Tricks, Tests and Puzzles — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "The Complete Book of Fun Maths: 250 Confidence-boosting Tricks, Tests and Puzzles" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

1234567...25

Table of Contents

Titles inThe IQ Workout Series

Increase Your Brainpower: Improve your creativity, memory, mental agility and intelligence 0-471-53123-5

Maximize Your Brainpower: 1000 new ways to boost your mental fitness 0-470-84716-6

IQ Testing: 400 ways to evaluate your brainpower 0-471-53145-6

More IQ Testing: 250 new ways to release your IQ potential 0-470-84717-4

Psychometric Testing: 1000 ways to assess your personality, creativity, intelligence and lateral thinking 0-471-52376-3

More Psychometric Testing: 1000 new ways to assess your personality, creativity, intelligence and lateral thinking 0-470-85039-6

Introduction

Im very well acquainted too with matters mathematical,
I understand equations, both the simple and quadratical.

W. S. Gilbert

Bertrand Russell once said that Mathematics may be defined as the subject in which we never know what we are talking about, nor whether what we are saying is true.

The subject of mathematics can be challenging, fascinating, confusing and frustrating, but once you have developed an interest in the science of numbers, a whole new world is opened up as you discover their many characteristics and patterns.

We all require some numerical skills in our lives, whether it is to calculate our weekly shopping bill or to budget how to use our monthly income, but for many people mathematics is a subject they regard as being too difficult when confronted by what are considered to be its higher branches. When broken down and analysed, and explained in laymans terms, however, many of these aspects can be readily understood by those of us with only a rudimentary grasp of the subject.

The basic purpose of this book is to build up readers confidence with maths by means of a series of tests and puzzles, which become progressively more difficult over the course of the book, starting with the gentle Work out of Chapter 1 to the collection of Complexities and curiosities of Chapter 8. There is also the opportunity, in Chapter 3, for readers to test their numerical IQ. For many of the puzzles throughout the book, hints towards finding a solution are provided, and in all cases the answers come complete with full detailed explanations.

Many of the problems in this book are challenging, but deliberately so, as the more you practise on this type of puzzle, the more you will come to understand the methodology and thought processes necessary to solve them and the more proficient you will become at arriving at the correct solution. Of equal importance, we set out to show that dealing with numbers can be great fun, and to obtain an understanding of the various aspects of mathematics in an entertaining and informative way can be an uplifting experience.

Section 1

Puzzles, tricks and tests

Chapter 1

The work out

All intellectual improvement arises from leisure.

Samuel Johnson

Every work out, be it physical or mental, involves a limbering up session.

The puzzles in this chapter are such a limbering up session. They have been specially selected to get you to think numerically and to increase your confidence when working with numbers or faced with a situation in which a mathematical calculation is required, and, like all the puzzles in this book, they are there to amuse and entertain.

When looking at a puzzle, the answer may hit you immediately. If not, your mind must work harder at exploring the options. Mathematics is an exact science, and there is only one correct solution to a correctly set question or puzzle; however, there may be different methods of arriving at that solution, some more laborious than others.

As you work through this first chapter you will find that there are many different ways of tackling this type of puzzle and arriving at a solution, whether it be by logical analysis or by intelligent trial and error.

1. Two golfers were discussing what might have been after they had played a par 5.

Harry said if I had taken one shot less and you had taken one shot more, we would have shared the hole.

Geoff then countered by saying yes, and if I had taken one shot less and you had taken one shot more you would have taken twice as many shots as me.

How many shots did each take?

2. A number between 1 and 50 meets the following criteria:

it is divisible by 3
when the digits are added together the total is between 4 and 8
it is an odd number
when the digits are multiplied together the total is between 4 and 8.

What is the number?

3. On arriving at the party the six guests all say Hello to each other once.

On leaving the party the six guests all shake hands with each other once.

How many handshakes is that in total, and how many Hellos?

4. What two numbers multiplied together equal 13?

5. Working at the stable there are a number of lads and lasses looking after the horses. In all there are 22 heads and 72 feet, including all the lads and lasses plus the horses.

If all the lads and lasses and all the horses are sound in body and limb, how many humans and how many horses are in the stable?

6. How many boxes measuring 1 m 1 m 50 cm can be packed into a container measuring 6 m 5 m 4 m?

7. By what fractional part does four-quarters exceed three-quarters?

8.

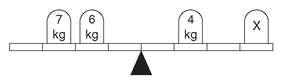
What weight should be placed on x in order to balance the scale?

9. My house number is the lowest number on the street that, when divided by 2, 3, 4, 5 or 6, will always leave a remainder of 1.

However, when divided by 11 there is no remainder.

What is my house number?

10. My brother is less than 70 years old.

The number of his age is equal to five times the sum of its digits. In 9 years time the order of the digits of his age now will be reversed.

How old is my brother now?

11. A greengrocer received a boxful of Brussels sprouts and was furious upon opening the box to find that several had gone bad.

He then counted them up so that he could make a formal complaint and found that 114 were bad, which was 8 per cent of the total contents of the box.

How many sprouts were in the box?

12. If seven men can build a house in 15 days, how long will it take 12 men to build a house assuming all men work at the same rate?

13. At the end of the day one market stall has eight oranges and 24 apples left. Another market stall has 18 oranges and 12 apples left.

What is the difference between the percentages of oranges left in each market stall?

14. Peter is twice as old as Paul was when Peter was as old as Paul is now.

The combined ages of Peter and Paul is 56 years.

How old are Peter and Paul now?

The next two puzzles are of a very similar nature.

15. A bag of potatoes weighs 25 kg divided by a quarter of its weight. How much does the bag of potatoes weigh?

16. One bag of potatoes weighed 60 kg plus one-quarter of its own weight and the other bag weighed 64 kg plus one-fifth of its own weight.Which is the heavier bag?

Next page

1234567...25

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

Similar books «The Complete Book of Fun Maths: 250 Confidence-boosting Tricks, Tests and Puzzles»

Look at similar books to The Complete Book of Fun Maths: 250 Confidence-boosting Tricks, Tests and Puzzles. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.

Norvin Pallas

Calculator Puzzles, Tricks and Games

Sam Loman

Fairy Puzzles

Lisa Regan

Super Logic Puzzles

Jerome S. Meyer

Puzzles, Games, & Tricks: Understanding the Mystery and Magic of Numbers

On Target Puzzles

140 Photography Puzzles: Photo Themed Word Search, Word Scramble and Cryptogram Puzzles For Photography Enthusiasts

Arcturus Publishing

Lateral Thinking Puzzles

Jason Rosenhouse

Games for Your Mind: The History and Future of Logic Puzzles

Aland Johnson

Ultimate Logic Puzzles For Adults : Hack Your Brain With Challenging Numbers Logic Puzzles in Large Print for Fun Effective Brain Exercise

Carter Philip

The Complete Book of Fun Maths: 250 Confidence-Boosting Tricks, Tests and Puzzles

Gareth Moore

10-Minute Brain Teasers: Brain-Training Tips, Logic Tests, and Puzzles to Exercise Your Mind

Ian Livingstone

Brain Teasers: 211 Logic Puzzles, Lateral Thinking Games, Mazes, Crosswords, and IQ Tests to Exercise Your Mind and Keep You Sharp til Youre 100

Anany Levitin

Algorithmic Puzzles

Discussion, reviews of the book The Complete Book of Fun Maths: 250 Confidence-boosting Tricks, Tests and Puzzles and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.