Sushil C. Dimri - Algorithms

De Gruyter Textbook

ISBN 9783110693416

e-ISBN (PDF) 9783110693607

e-ISBN (EPUB) 9783110693751

Bibliographic information published by the Deutsche Nationalbibliothek

The Deutsche Nationalbibliothek lists this publication in the Deutsche Nationalbibliografie; detailed bibliographic data are available on the Internet at http://dnb.dnb.de.

2021 Walter de Gruyter GmbH, Berlin/Boston

An algorithm is a finite sequence of computational steps that produces the desired output when applied on a certain problem with necessary input values. In algorithm, every step must be clear, simple, definite, and unambiguous. shows diagrammatic representation of algorithm.

Figure 1.1: Algorithm.

An algorithm is defined as an ultimate group of instructions to achieve a given set of goals to fulfill the given criteria.

1. Input: Zero or more quantities must be passed externally as input to algorithm.

2. Output: Minimum one quantity must be formed as an output.

3. Finiteness: An algorithm must be well defined in a finite set of steps.

4. Definiteness: Each and every instruction of a given algorithm must be precise and unambiguous.

5. Effectiveness: Every statement/instruction specifically contributes something in solution, defined by an algorithm.

Example 1.1: We will discuss an example of a sorting algorithm.

Input: Set of elements (sequence)

where elements are in random fashion.

Output: Elements in ascending order, that is:

Analysis of the algorithms allows us to take decisions about the value of one algorithm over another. When an algorithm is executed in computer, it requires central processing unit (CPU, for performing its operations) and memory (for storing program and data). There are two parameters on which we can analyze the performance of an algorithm. These are time complexity and space complexity. As compared to space analysis, the analysis of time requirements for an algorithm is important, but whenever necessary, both the complexities are used.

The amount of memory required by a program to run to conclusion is known as space complexity. Space is a kind of resource that is reusable, and we can easily increase the space (memory) of the system. But time is a resource that is limited, not reusable, and nonpurchasable.

Time complexity completely relies on the size of the input. The sum of time of CPU needed by the algorithm (program) to execute to conclusion is known as time complexity. It should be noted that the same algorithm can take different time to run. There are three kinds of time complexity: best, worst, and average case complexity of the algorithm. Best-case complexity is the minimum amount of time taken by the algorithm for n-sized input. Average-case complexity is the time taken by the algorithm having typical input data of size n. Worst-case complexity is the maximum amount of time required by the algorithm for n-sized input. These terms will be discussed later in this chapter.

The time complexity of an algorithm is generally a function of the input size n. Growth order of a function indicates how fast a function grows with respect to change in input size n. Some useful popular functions are:

• Linear function: n

• Square function: n2

• Exponential function: 2n

• Logarithmic function: log2n

shows how various functions grow with the input size n. The graph is evidence for how fast exponential function grows in comparison to other functions.

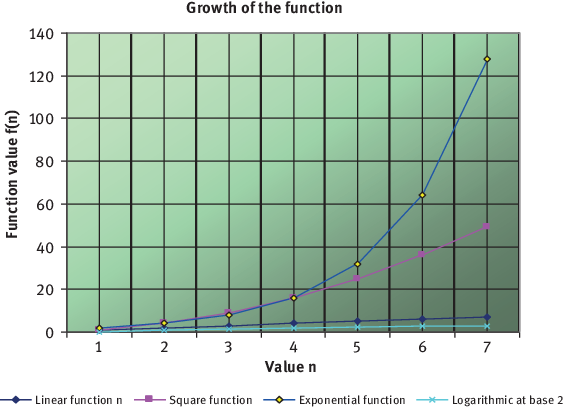
Figure 1.2: Plotting function values.

Whenever we learn about an algorithm, we are keen to depict them as per their preciseness and efficiency. In other words, we are mainly concerned about the growth of the running time of an algorithm (not in the exact running time). Scientifically, this phenomenon is called asymptotic running time. There is an acute need to design a method to find out the rate of growth of functions so that we can compare algorithms. Asymptotic notation is an innovative way to provide the suitable methodology for categorizing functions according to the rate of growth of function.

Let f(n) and g(n) are two positive functions. A function f(n) is said to be in O(g(n)) signified by f(n)=O(g(n)). If f(n) is bounded above by some positive constant multiple of g(n) for large values of n, i.e. there exists some positive constant c and some nonnegative whole number n0 (allude ) with the end goal that

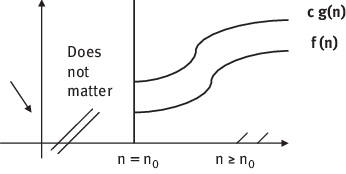
Figure 1.3: Growth of the Function f(n) and g(n) for Big oh notation.

Example 1.2:

500 n+1=f(n) says

500 n+1500 n+n{ n1}

501 n501 n2

500 n+1501 n2, n1

So c=501, and n0=1

500 n+1O(n2)

Let f(n) and g(n) are two positive functions. The function f(n) is said to be in (g(n)) (Omega of g(n)) meant by f(n)=(g(n)); if function f(n) is lower bounded by some positive multiple of g(n) for some large value of n, i.e. there exist a positive constant c and some nonnegative whole number n0 (allude ), with the end goal that

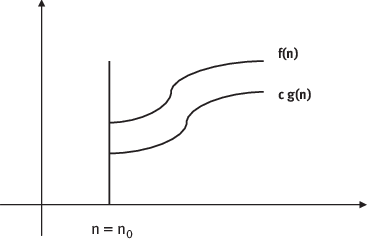
Figure 1.4: Growth of the Function f(n) and g(n) for Omega notation.

Example 1.3:

f(n)=(n3)

g(n)=(n2)

n3n2 v n0

n31.n2,where n00

Hence, c=1, n0=0, n3(n2)

Let f(n) and g(n) are two positive functions. A function f(n) is said to be in (g(n)) (Theta of g(n)), which means f(n)=(g(n)). The function f(n) is limited above and below by some positive constant multiple of g(n) for large value of n, i.e. there exist positive constants c1 and c2 and some nonnegative whole number n0 (allude ), with the end goal that

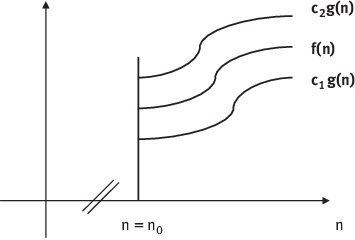
Figure 1.5: Growth of the Function f(n) and g(n) for Theta notation.

Example 1.4:

For upper bound:

For lower bound:

So, we have

This implies that

Theorem 1.1: