
Milo Beckman
MATH WITHOUT NUMBERS
Illustrated by M Erazo

Contents
- Foundations :
a dialog
About the Author
Milo Beckman is a maths prodigy from New York. His diverse projects and independent research have been featured in the The New York Times, FiveThirtyEight, the Huffington Post, Business Insider, the Economist, and others. He worked for three tech companies, two banks, and a US Senator before retiring at age nineteen to teach math in New York, China, and Brazil, and to write.
About the Illustrator
The role of the artist is to make the revolution irresistible.
Toni Cade Bambara
M is a brown genderqueer cultural worker and organizer. Under the name Emulsify, they create art that helps them heal, learn, advocate, and imagine new worlds. They believe all art is powerful and political. M lives in Brooklyn with their wife and spends a lot of time creating while snuggling their pups. Ms creative energy and love are a part of all they do: they are a trained abortion doula, founder of Emulsify Design, and creative director of Arrebato, a space for Queer Trans Black & Brown community. Through their work, M has made incredible friendships, learned from brilliant peers, and found their home. You can follow Ms work on their website at emulsify.art.
to Eriq, for making me do this
with thanks to Taylor for checking my math, Portia for the dialog, and M for bringing it to life

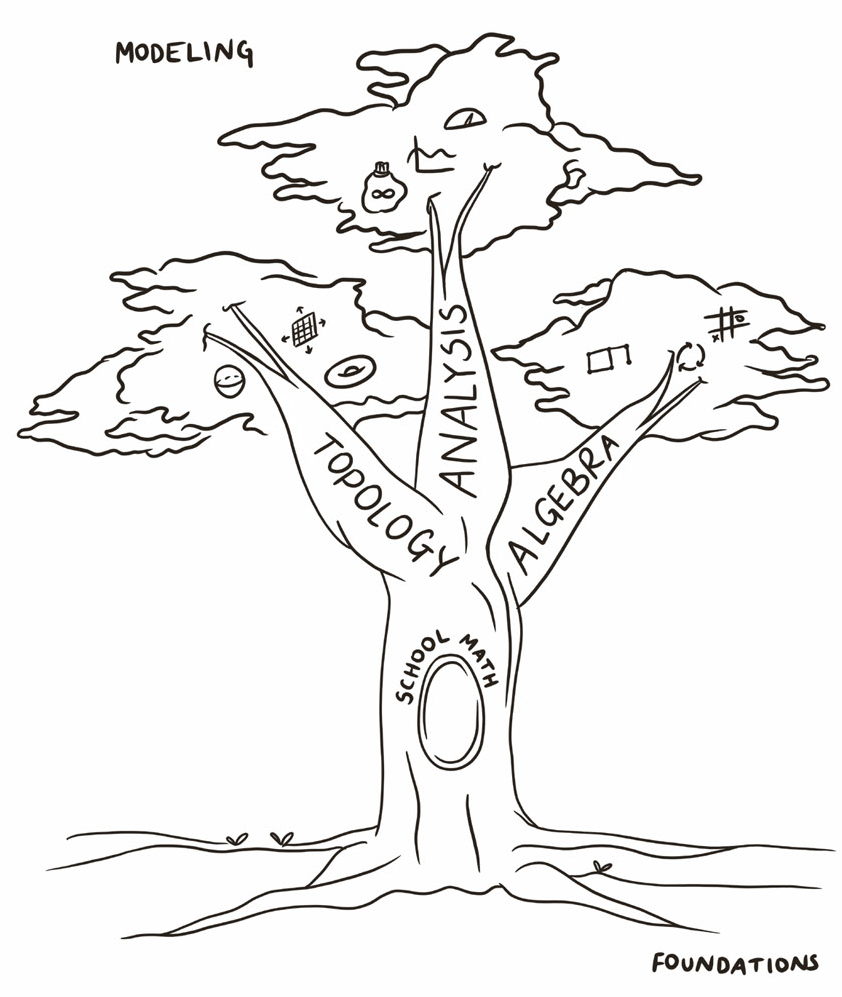
what do mathematicians believe?

We believe math is interesting, true, and useful (in that order).
We believe in a process called mathematical proof. We believe the knowledge produced by proof is important and powerful.
Fundamentalist mathematicians believe that everythingplants, love, music, everythingcan (in theory) be understood in terms of math.


TOPOLOGY

shape
Mathematicians like to overthink things. Its sort of what we do. We take some concept that everyone understands on a basic level, like symmetry or equality, and pick it apart, trying to find a deeper meaning to it.
Take shape. We all know more or less what a shape is. You look at an object and you can easily tell if its a circle or a rectangle or whatever else. But a mathematician would ask: What is a shape? What makes something the shape it is? When you identify an object by shape, youre ignoring its size, its color, what its used for, how old it is, how heavy it is, who brought it here, and whos responsible for taking it home when we leave. What are you not ignoring? What is it that youre getting across when you say something is shaped like a circle?
These questions are, of course, pointless. For all practical uses, your intuitive understanding of shape is fineno significant decision in your life will ever hinge on how exactly we define the word shape. Its just an interesting thing to think about, if you have some extra time and you want to spend it thinking about shapes.
Lets say you do. Heres a question you might think to ask yourself:

How many shapes are there?
Its a simple enough question, but it isnt easy to answer. A more precise and limited version of this question, called the generalized Poincar conjecture, has been around for well over a century and we still dont know of anyone whos been able to solve it. Lots of people have tried, and one professional mathematician recently won a million-dollar prize for finishing up a big chunk of the problem. But there are still many categories of shapes left uncounted, so we still dont know, as a global community, how many shapes there are.
Lets try to answer the question. How many shapes are there? For lack of a better idea, it seems like a useful thing to do to just start drawing shapes and see where that takes us.
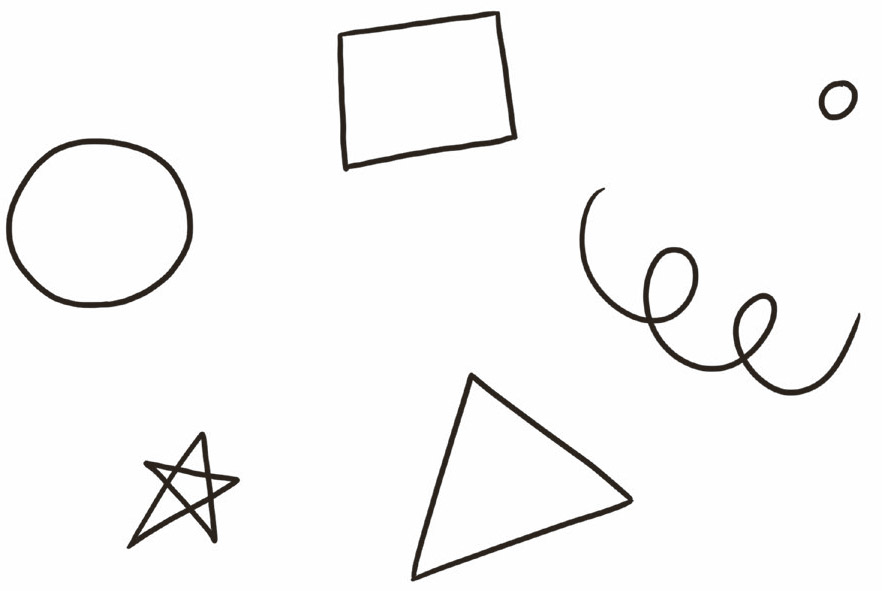

It looks like the answer to our question is going to depend on how exactly we divide things into different shape categories. Is a big circle the same shape as a small circle? Are we counting squiggle as one big category, or should we split them up based on the different ways they squiggle? We need a general rule to settle debates like this, so the question of how many shapes wont come down to case-by-case judgment calls.
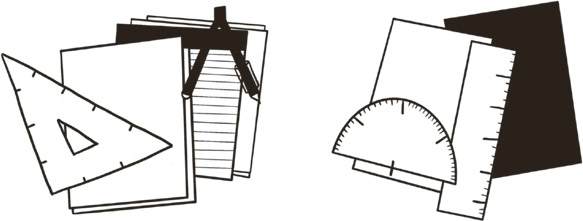
There are several rules we could pick here that would all do a fine job of deciding when two shapes are the same or different. If youre a carpenter or an engineer, youll want a very strict and precise rule, one that calls two shapes the same only if all their lengths and angles and curves match up perfectly. That rule leads to a kind of math called geometry, where shapes are rigid and exact and you do things like draw perpendicular lines and calculate areas.
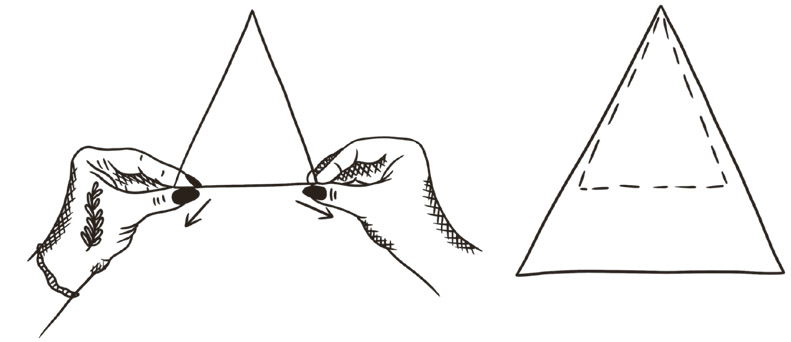
We want something a little looser. Were trying to find every possible shape, and we dont have time to sort through thousands of different variations of squiggles. We want a rule thats generous about when to consider two things the same shape, that breaks up the world of shapes into a manageable number of broad categories.

Two shapes are the same if you can turn one into the other by stretching and squeezing, without any ripping or gluing.

This rule is the central idea of topology, which is like a looser, trippier version of geometry. In topology, shapes are made out of a thin, endlessly stretchy material that you can twist and pull and manipulate like gum or dough. In topology, the size of a shape doesnt matter.
 Next page
Next page
























