

Library of Congress Control Number:2019953072 Copyright 2020, Prufrock Press Inc. Edited by Katy McDowall Cover and layout design by Allegra Denbo ePub ISBN: 978-1-64632-015-8 No part of this book may be reproduced, translated, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, microfilming, recording, or otherwise, without written permission from the publisher. For more information about our copyright policy or to request reprint permissions, visit https://www.prufrock.com/permissions.aspx. At the time of this books publication, all facts and figures cited are the most current available. All telephone numbers, addresses, and website URLs are accurate and active. All publications, organizations, websites, and other resources exist as described in the book, and all have been verified.
The author and Prufrock Press Inc. make no warranty or guarantee concerning the information and materials given out by organizations or content found at websites, and we are not responsible for any changes that occur after this books publication. If you find an error, please contact Prufrock Press Inc.
 | Prufrock Press Inc.
P.O. Box 8813
Waco, TX 76714-8813
Phone: (800) 998-2208
Fax: (800) 240-0333
http://www.prufrock.com |
With many thanks to ohn Fitzgerald, Rebecca McCormick, and Sheliah Shepard Dedicated with love to: John Joel Fitzgerald, my husband, and Amanda Therese Fitzgerald, our daughter (December 5, 1981March 31, 2002) Table of Contents Introduction T here are many keys to being a proficient math problem solver, and two of the most important elements to successful problem solving are knowing: what the problem is asking (understanding the vocabulary and being able to determine which strategy to employ), and how to perform the operation(s) (being able to quickly and automatically perform the necessary operations).
Stress-Free Math is much more than a compilation of words and definitions.
Stress-Free Math is much more than a compilation of words and definitions.
This book has been organized to reflect the different areas of mathematics taught in elementary and junior high schools. Each category includes the terms commonly used in this field of study, concise definitions, and many examples and illustrations. In addition, the book provides quick reference guides for basic operations and tables of commonly used facts and equivalents. Once you use a reference like this book, youll agree that it truly is absolutely essential. It will be the reference material you will use again and again to supplement and reinforce topics throughout your math classes. Visual Definitions by Topic  WHOLE NUMBERS AND OPERATIONS Addends Numbers in addition problems that are added together to form a sum.
WHOLE NUMBERS AND OPERATIONS Addends Numbers in addition problems that are added together to form a sum.
Example: 3 + 7 = 10 3 and 7 are addends. Addition The process of uniting two or more numbers into a sum; counting the total. Key word: altogether Examples:  Arabic Numbers A Base-10 place-value number system that uses the symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Also called Hindu-Arabic numbers. Arithmetic Progression A series of numbers in which each number differs from the preceding number by a fixed amount. A series of numbers that follows a pattern.
Arabic Numbers A Base-10 place-value number system that uses the symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Also called Hindu-Arabic numbers. Arithmetic Progression A series of numbers in which each number differs from the preceding number by a fixed amount. A series of numbers that follows a pattern.
Example: 1, 5, 9, 13, 17, 21, 25, 29,... Each number differs by 4. Array An organized arrangement of objects using rows and columns. These can be very helpful in building multiplication problems and division problems. Example 1: 6 rows of 7 columns = 42 squares altogether 6 x 7 = 42 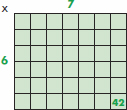 Example 2: Build the problem 20 4 in an array using as many of the 20 tiles as you can. 20 4 = 5. 20 4 = 5.
Example 2: Build the problem 20 4 in an array using as many of the 20 tiles as you can. 20 4 = 5. 20 4 = 5.
There is no remainder in this problem. 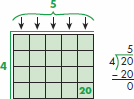 Example 3: Count out 21 tiles. Build the problem 21 4 in an array using as many of the 20 tiles as you can. In this case, 20 tiles can be used to build the array with 1 tile left over. Count the number of rows that have been built, and count the remainder. 20 4 = 5.
Example 3: Count out 21 tiles. Build the problem 21 4 in an array using as many of the 20 tiles as you can. In this case, 20 tiles can be used to build the array with 1 tile left over. Count the number of rows that have been built, and count the remainder. 20 4 = 5.
There is 1 remainder. Write the remainder as a fraction. 21 4 = 5 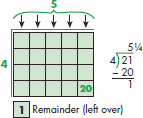 Ascend To increase in number, value, or amount. Ascending Order Increasing from least to greatest, but not necessarily according to a fixed pattern. To count upward from smallest to largest; counting up. Examples: 35, 37, 39, 41, 43, 45, 47, 49,...
Ascend To increase in number, value, or amount. Ascending Order Increasing from least to greatest, but not necessarily according to a fixed pattern. To count upward from smallest to largest; counting up. Examples: 35, 37, 39, 41, 43, 45, 47, 49,...
An example of an ascending arithmetic progression. 1, 5, 13, 40, 53 A series of numbers in ascending order. Binary Numbers A numerical system that is based on the number 2. Each place has a value equal to a power of 2, as indicated or shown by the symbols 0 or 1.  Cardinal Numbers Numbers used for counting or answering the question how many?; they show quantity. Key words: counting numbers Example: Numbers such as 1, 2, 3, 47, and 104 are cardinal numbers.
Cardinal Numbers Numbers used for counting or answering the question how many?; they show quantity. Key words: counting numbers Example: Numbers such as 1, 2, 3, 47, and 104 are cardinal numbers.
Common Factor/Common Divisor A factor that two or more numbers have in common. A number that divides two or more numbers evenly (without a remainder). Example 1: When using tiles to look at two numbers, the common factors are the factors that both numbers share. 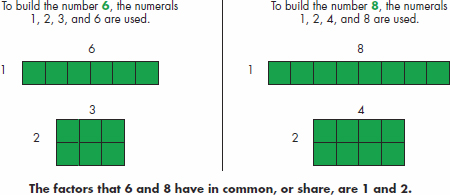 Example 2:
Example 2: 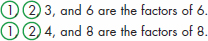 The factors that 6 and 8 have in common, or share, are 1 and 2. Common Multiple Any number that is a multiple of two or more numbers; a multiple that two or more numbers have in common, or share. Key words: common, shared Example:
The factors that 6 and 8 have in common, or share, are 1 and 2. Common Multiple Any number that is a multiple of two or more numbers; a multiple that two or more numbers have in common, or share. Key words: common, shared Example: 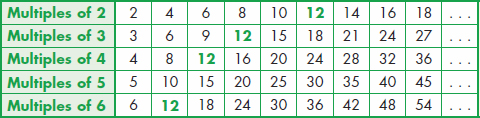 is a common multiple of 2, 3, 4, and 6.
is a common multiple of 2, 3, 4, and 6.
Composing Numbers The process of creating a larger number through addition. Example: 1,000 + 300 + 10 + 7 is composed as 1,317. Composite Number A number that has factors other than 1 and itself. A number that can be built in more than one way using tiles. Composite numbers can be written as the product of prime numbers. Example: 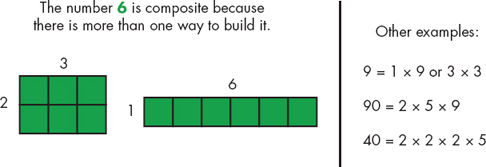















 Library of Congress Control Number:2019953072 Copyright 2020, Prufrock Press Inc. Edited by Katy McDowall Cover and layout design by Allegra Denbo ePub ISBN: 978-1-64632-015-8 No part of this book may be reproduced, translated, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, microfilming, recording, or otherwise, without written permission from the publisher. For more information about our copyright policy or to request reprint permissions, visit https://www.prufrock.com/permissions.aspx. At the time of this books publication, all facts and figures cited are the most current available. All telephone numbers, addresses, and website URLs are accurate and active. All publications, organizations, websites, and other resources exist as described in the book, and all have been verified.
Library of Congress Control Number:2019953072 Copyright 2020, Prufrock Press Inc. Edited by Katy McDowall Cover and layout design by Allegra Denbo ePub ISBN: 978-1-64632-015-8 No part of this book may be reproduced, translated, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, microfilming, recording, or otherwise, without written permission from the publisher. For more information about our copyright policy or to request reprint permissions, visit https://www.prufrock.com/permissions.aspx. At the time of this books publication, all facts and figures cited are the most current available. All telephone numbers, addresses, and website URLs are accurate and active. All publications, organizations, websites, and other resources exist as described in the book, and all have been verified. 
 WHOLE NUMBERS AND OPERATIONS Addends Numbers in addition problems that are added together to form a sum.
WHOLE NUMBERS AND OPERATIONS Addends Numbers in addition problems that are added together to form a sum. Arabic Numbers A Base-10 place-value number system that uses the symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Also called Hindu-Arabic numbers. Arithmetic Progression A series of numbers in which each number differs from the preceding number by a fixed amount. A series of numbers that follows a pattern.
Arabic Numbers A Base-10 place-value number system that uses the symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Also called Hindu-Arabic numbers. Arithmetic Progression A series of numbers in which each number differs from the preceding number by a fixed amount. A series of numbers that follows a pattern. Example 2: Build the problem 20 4 in an array using as many of the 20 tiles as you can. 20 4 = 5. 20 4 = 5.
Example 2: Build the problem 20 4 in an array using as many of the 20 tiles as you can. 20 4 = 5. 20 4 = 5. Example 3: Count out 21 tiles. Build the problem 21 4 in an array using as many of the 20 tiles as you can. In this case, 20 tiles can be used to build the array with 1 tile left over. Count the number of rows that have been built, and count the remainder. 20 4 = 5.
Example 3: Count out 21 tiles. Build the problem 21 4 in an array using as many of the 20 tiles as you can. In this case, 20 tiles can be used to build the array with 1 tile left over. Count the number of rows that have been built, and count the remainder. 20 4 = 5. Ascend To increase in number, value, or amount. Ascending Order Increasing from least to greatest, but not necessarily according to a fixed pattern. To count upward from smallest to largest; counting up. Examples: 35, 37, 39, 41, 43, 45, 47, 49,...
Ascend To increase in number, value, or amount. Ascending Order Increasing from least to greatest, but not necessarily according to a fixed pattern. To count upward from smallest to largest; counting up. Examples: 35, 37, 39, 41, 43, 45, 47, 49,... Cardinal Numbers Numbers used for counting or answering the question how many?; they show quantity. Key words: counting numbers Example: Numbers such as 1, 2, 3, 47, and 104 are cardinal numbers.
Cardinal Numbers Numbers used for counting or answering the question how many?; they show quantity. Key words: counting numbers Example: Numbers such as 1, 2, 3, 47, and 104 are cardinal numbers. Example 2:
Example 2: 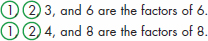 The factors that 6 and 8 have in common, or share, are 1 and 2. Common Multiple Any number that is a multiple of two or more numbers; a multiple that two or more numbers have in common, or share. Key words: common, shared Example:
The factors that 6 and 8 have in common, or share, are 1 and 2. Common Multiple Any number that is a multiple of two or more numbers; a multiple that two or more numbers have in common, or share. Key words: common, shared Example:  is a common multiple of 2, 3, 4, and 6.
is a common multiple of 2, 3, 4, and 6.