A HISTORY OF
MATHEMATICAL NOTATIONS
FLORIAN CAJORI
Two Volumes Bound As One
Volume I:
Notations in Elementary Mathematics
Volume II:
Notations Mainly in Higher Mathematics
DOVER PUBLICATIONS, INC.
Mineola, New York
Bibliographical Note
This Dover edition, first published in 1993, and reissued in 2012, is an unabridged and unaltered republication in one volume of the work first published in two volumes by The Open Court Publishing Company, La Salle, Illinois, in 1928 and 1929.
Library of Congress Cataloging-in-Publication Data
Cajori, Florian, 1859-1930.
A history of mathematical notations / by Florian Cajori.
p. cm.
Originally published: Chicago : Open Court Pub. Co., 1928-1929.
Two volumes bound as one.
Includes indexes.
Contents: v. 1. Notations in elementary mathematics v. 2. Notations mainly in higher mathematics.
ISBN-13: 978-0-486-67766-8
ISBN-10: 0-486-67766-4
1. Mathematical notationHistory. 2. MathematicsHistory. 3. NumeralsHistory. I. Title.
QA41.C32 1993
510.148dc20
93-29211
CIP
Manufactured in the United States by Courier Corporation
67766404
www.doverpublications.com
PREFACE
The study of the history of mathematical notations was suggested to me by Professor E. H. Moore, of the University of Chicago. To him and to Professor M.W. Haskell, of the University of California, I am indebted for encouragement in the pursuit of this research. As completed in August, 1925, the present history was intended to be brought out in one volume. To Professor H. E. Slaught, of the University of Chicago, I owe the suggestion that the work be divided into two volumes, of which the first should limit itself to the history of symbols in elementary mathematics, since such a volume would appeal to a wider constituency of readers than would be the case with the part on symbols in higher mathematics. To Professor Slaught I also owe generous and vital assistance in many other ways. He examined the entire manuscript of this work in detail, and brought it to the sympathetic attention of the Open Court Publishing Company. I desire to record my gratitude to Mrs. Mary Hegeler Carus, president of the Open Court Publishing Company, for undertaking this expensive publication from which no financial profits can be expected to accrue.
I gratefully acknowledge the assistance in the reading of the proofs of part of this history rendered by Professor Haskell, of the University of California; Professor R. C. Archibald, of Brown University; and Professor L. C. Karpinski, of the University of Michigan.
F LORIAN C AJORI
U NIVERSITY OF C ALIFORNIA
TABLE OF CONTENTS
ByzantineMaximus Planudes, Fourteenth Century
EnglishJohn Wallis, 1655, 1657, 1685
Notations for Geometric Ratio
Double Significance of R and l
Crossed Numerals Representing Powers of Unknowns
ILLUSTRATIONS
R EAL E STATE S ALE , M EXICO C ITY , 1718
F ROM C HR . R UDOLFF S Coss, E V
R ADICALS IN J. H UME , 1635
Volume I
NOTATIONS IN ELEMENTARY MATHEMATICS
I
INTRODUCTION
In this history it has been an aim to give not only the first appearance of a symbol and its origin (whenever possible), but also to indicate the competition encountered and the spread of the symbol among writers in different countries. It is the latter part of our program which has given bulk to this history.
The rise of certain symbols, their day of popularity, and their eventual decline constitute in many cases an interesting story. Our endeavor has been to do justice to obsolete and obsolescent notations, as well as to those which have survived and enjoy the favor of mathematicians of the present moment.
If the object of this history of notations were simply to present an array of facts, more or less interesting to some students of mathematicsif, in other words, this undertaking had no ulterior motivethen indeed the wisdom of preparing and publishing so large a book might be questioned. But the author believes that this history constitutes a mirror of past and present conditions in mathematics which can be made to bear on the notational problems now confronting mathematics. The successes and failures of the past will contribute to a more speedy solution of the notational problems of the present time.
II
NUMERAL SYMBOLS AND COMBINATIONS OF SYMBOLS
BABYLONIANS
1. In the Babylonian notation of numbers a vertical wedge  stood for 1, while the characters
stood for 1, while the characters 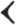 and
and 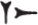 signified 10 and 100, respectively. Grotefend believes the character for 10 originally to have been the picture of two hands, as held in prayer, the palms being pressed together, the fingers close to each other, but the thumbs thrust out. Ordinarily, two principles were employed in the Babylonial notationthe additive and multiplicative. We shall see that limited use was made of a third principle, that of subtraction.
signified 10 and 100, respectively. Grotefend believes the character for 10 originally to have been the picture of two hands, as held in prayer, the palms being pressed together, the fingers close to each other, but the thumbs thrust out. Ordinarily, two principles were employed in the Babylonial notationthe additive and multiplicative. We shall see that limited use was made of a third principle, that of subtraction.
2. Numbers below 200 were expressed ordinarily by symbols whose respective values were to be added. Thus, 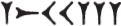 stands for 123. The principle of multiplication reveals itself in
stands for 123. The principle of multiplication reveals itself in 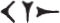 where the smaller symbol 10, placed before the 100, is to be multiplied by 100, so that this symbolism designates 1,000.
where the smaller symbol 10, placed before the 100, is to be multiplied by 100, so that this symbolism designates 1,000.
3. These cuneiform symbols were probably invented by the early Sumerians. Their inscriptions disclose the use of a decimal scale of numbers and also of a sexagesimal scale.
Early Sumerian clay tablets contain also numerals expressed by circles and curved signs, made with the blunt circular end of a stylus, the ordinary wedge-shaped characters being made with the pointed end. A circle  stood for 10, a semicircular or lunar sign stood for 1. Thus, a round-up of cattle shows
stood for 10, a semicircular or lunar sign stood for 1. Thus, a round-up of cattle shows  , or 36, cows.
, or 36, cows.
4. The sexagesimal scale was first discovered on a tablet by E. Hincksof the moons disk for every day from new to full moon, the whole disk being assumed to consist of 240 parts. The illuminated parts during the first five days are the series 5, 10, 20, 40, 1.20, which is a geometrical progression, on the assumption that the last number is 80. From here on the series becomes arithmetical, 1.20, 1.36, 1.52, 2.8, 2.24, 2.40, 2.56, 3.12, 3.28, 3.44, 4, the common difference being 16. The last number is written in the tablet  , and, according to Hinckss interpretation, stood for 4 60 = 240.
, and, according to Hinckss interpretation, stood for 4 60 = 240.
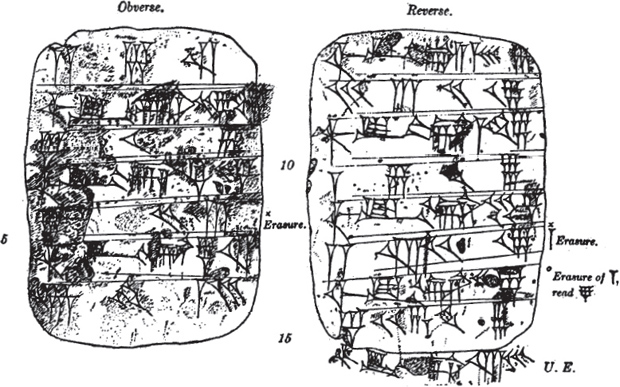
F IG . 1Babylonian tablets from Nippur, about 2400 B.C.
5. Hinckss explanation was confirmed by the decipherment of tablets found at Senkereh, near Babylon, in 1854, and called the Tablets of Senkereh. One tablet was found to contain a table of square numbers, from 12 to 602, a second one a table of cube numbers from 13 to 323. The tablets were probably written between 2300 and 1600 B.C. Various scholars contributed toward their interpretation. Among them were George Smith (1872), J. Oppert, Sir H. Rawlinson, Fr. Lenormant, and finally R. Lepsius.and 49 are given as the squares of the first seven integers, respectively. We have next 1.4 = 82, 1.21 = 92, 1.40 = 102, etc. This clearly indicates the use of the sexagesimal scale which makes 1.4 = 60 + 4, 1.21 = 60 + 21, 1.40 = 60 + 40, etc. This sexagesimal system marks the earliest appearance of the all-important principle of position in writing numbers. In its general and systematic application, this principle requires a symbol for zero. But no such symbol has been found on early Babylonian tablets; records of about 200 B.C. give a symbol for zero, as we shall see later, but it was not used in calculation. The earliest thorough and systematic application of a symbol for zero and the principle of position was made by the Maya of Central America, about the beginning of the Christian Era.
Next page










 stood for 1, while the characters
stood for 1, while the characters 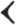 and
and 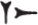 signified 10 and 100, respectively. Grotefend believes the character for 10 originally to have been the picture of two hands, as held in prayer, the palms being pressed together, the fingers close to each other, but the thumbs thrust out. Ordinarily, two principles were employed in the Babylonial notationthe additive and multiplicative. We shall see that limited use was made of a third principle, that of subtraction.
signified 10 and 100, respectively. Grotefend believes the character for 10 originally to have been the picture of two hands, as held in prayer, the palms being pressed together, the fingers close to each other, but the thumbs thrust out. Ordinarily, two principles were employed in the Babylonial notationthe additive and multiplicative. We shall see that limited use was made of a third principle, that of subtraction.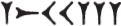 stands for 123. The principle of multiplication reveals itself in
stands for 123. The principle of multiplication reveals itself in 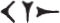 where the smaller symbol 10, placed before the 100, is to be multiplied by 100, so that this symbolism designates 1,000.
where the smaller symbol 10, placed before the 100, is to be multiplied by 100, so that this symbolism designates 1,000. stood for 10, a semicircular or lunar sign stood for 1. Thus, a round-up of cattle shows
stood for 10, a semicircular or lunar sign stood for 1. Thus, a round-up of cattle shows  , or 36, cows.
, or 36, cows. , and, according to Hinckss interpretation, stood for 4 60 = 240.
, and, according to Hinckss interpretation, stood for 4 60 = 240.