Rona Gurkewitz - 3-D Geometric Origami
Here you can read online Rona Gurkewitz - 3-D Geometric Origami full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2012, publisher: INscribe Digital;Dover Publications, genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:3-D Geometric Origami
- Author:
- Publisher:INscribe Digital;Dover Publications
- Genre:
- Year:2012
- Rating:5 / 5
- Favourites:Add to favourites
- Your mark:
3-D Geometric Origami: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "3-D Geometric Origami" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Innovative, stimulating and challenging book combines the art of paperfolding with making polyhedra-based models. Projects range from the relatively simple cube and tetrahedron to such mind-boggling fabrications as the double pentagonal pyramid and the truncated hexadecahedron. Instructions and diagrams included.
Rona Gurkewitz: author's other books
Who wrote 3-D Geometric Origami? Find out the surname, the name of the author of the book and a list of all author's works by series.
3-D Geometric Origami — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "3-D Geometric Origami" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Font size:
Interval:
Bookmark:
This work was supported by a Connecticut State University/American Association of University Professors Research Grant 1993-1994.
Rona Gurkewitz is an Associate Professor of Mathematics and Computer Science at Western Connecticut State University. She became interested in origami in 1972 after meeting Laura Kruskal and Lillian Oppenheimer. Laura Kruskal is a creative folder and teacher and Lillian Oppenheimer was the founder of the Origami Center of America and was the International First Lady of Paperfolding during her lifetime.
A couple of years later, Rona became interested in polyhedra through a math education class taught by her colleague Stacey Wahl. Rona set about combining these two interests, and has shared geometric paper-folds with math teachers and others ever since. She has taught many classes, has had her work exhibited and has had folds published. She was a founding member of the Friends of the Origami Center of America (now called Origami U.S.A.) and served on its Board of Directors for five years.
Bennett Arnstein has been a mechanical-hardware engineer in the aerospace industry for over twenty years. He holds four patents. He became interested in polyhedra when he was ten years old. He has written three books, two of them on origami and polyhedra. One of these books was written with Lewis Simon, an eminent geometric designer and folder and a tremendous influence on Bennett. Bennett is a member of Origami U.S.A. and the West Coast Origami Guild and is a frequent contributor to their newsletters. He has done much teaching and exhibiting, as well as designing and folding origami models.
(Clockwise)
Truncated icosahedron
Truncated hexadecahedron
Dodecahedron
(All composed of One-Piece Triangle modules, page 37)
Cundy and Rollett, Mathematical Models , Oxford University Press, London, New York, 1961
Senechal and Fleck, eds., Shaping Space , A Polyhedral Approach , Birkhauser, Boston, 1988
Simon and Arnstein, Modular Origami Polyhedra , Bennett Arnstein, 1989 (ISBN 0-9620058-1-9)
Wenninger, Polyhedron Models , Cambridge University Press, New York, London, 1974.
Wenninger, Polyhedron Models for the Classroom , 1975, National Council of Teachers of Mathematics, 1906 Association Drive, Reston, Virginia 22091
There are many local groups in the U.S. that have meetings at which people get together to improve their folding. There also are international groups. Some of these groups have conventions and/or newsletters. If you have a computer, you can communicate with other folders through the Internet.
To access origami discussion by computer you will need a way of accessing the Internet. This can be done through an on-line service such as Compuserve, a service provider, or a school, university or workplace, with modern computer and communications software. Once on the net you can get subscription information by sending a message to:
maarten@info.service.rug.nl
The body of the message is faq (frequently asked questions). Discussions range over many topics including books, folds, mathematical origami and conventions. There is an archive site at rugcis.rug.nl which has all messages as well as articles, photos and more.
If you have access to the World Wide Web part of the internet, there are a number of origami home pages there. Joseph Wus page, which has been featured as a Cool Page of the Week, can be found at:
http://www.cs.ubc.ca/spider/jwu/origami.html.
The largest North American origami organization is Origami U.S.A. (formerly known as F.O.C.A.). It has a newsletter, an annual convention and special sessions throughout the year. It also has a mail-order operation featuring a large selection of origami books and paper. To find out about O.U.S.A. send a S.A.S.E. with two first-class stamps to 15 W. 77 St., N.Y., N.Y. 10024. It can also provide you with information about origami organizations all over the world.
Super Spike Ball, page 43
Put simply, a polyhedron is a three-dimensional figure made up of sides called faces, each face being a polygon. A polygon, in turn, is a two-dimensional figure made up of line segments, called edges, that are connected two at a time at their endpoints. In a polyhedron, several polygonal faces meet at a corner (vertex). When all the edges of the polygon are of equal length the polygon is called regular. An equilateral triangle and a square are examples of regular polygons made up of three and four edges respectively. A cube is a polyhedron with six square faces.
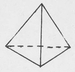
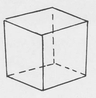
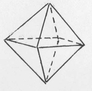
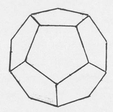
Polyhedra related to the models in this book are the Platonics, the Archi-medeans, the Kepler-Poinsot and some miscellaneous ones. Consider the Platonics. There are five of them, so named because they were known at the time of Plato (427?-347 B.C.). These polyhedra are also called regular polyhedra because they are made up of faces that are all the same regular polygon. The five Platonic polyhedra are the tetrahedron, the cube, the octahedron, the dodecahedron and the icosahedron. The tetrahedron is made from four equilateral triangles. The cube is made from six squares. The octahedron is made from eight equilateral triangles. Less familiar are the dodecahedron and the icosahedron. The dodecahedron is made from 12 regular pentagons with three meeting at each of 20 corners (vertices). The icosahedron is made from twenty equilateral triangles with five triangles meeting at each of 12 corners. The Platonics and the other polyhedra related to the origami models in this book are pictured and described in the pages immediately following.
Name: Tetrahedron
No. of faces: 4
Shape of faces: equilateral triangle
No. of edges: 6
No. of corners: 4
No. of edges or faces meeting at each corner: 3
Name: Cube
No. of faces: 6
Shape of faces: square
No. of edges: 12
No. of corners: 8
No. of edges or faces meeting at each corner: 3
Name: Octahedron
No. of faces: 8
Shape of faces: equilateral triangle
No. of edges: 12
No. of corners: 6
No. of edges or faces meeting at each corner: 4
Font size:
Interval:
Bookmark:
Similar books «3-D Geometric Origami»
Look at similar books to 3-D Geometric Origami. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
Discussion, reviews of the book 3-D Geometric Origami and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.