W. W. Sawyer - Prelude to Mathematics

No mathematician can be a complete mathematician unless he is also something of a poet.

K. Weierstrass

Wisdom is rooted in watching with affection the way people grow.

Confucius

This is a book about how to grow mathematicians. Probably you have no intention of trying to grow mathematicians. Even so, I hope you may find something of interest here. I myself have no intention of growing plants. I never do any gardening if I can possibly get out of it. But I like very much to look at gardens other people have grown. And I am still more interested if I can meet a man who will explain to me (what very few gardeners seem able to do) just how a plant grows; how, when it is a seed under the earth, it knows which way is up for its stem to grow, and which way is down for the roots; how a flower manages to face towards the light; what chemical elements the plant needs from the soil, and just how it manages to rearrange them into its own living tissue. The interest of these things is quite independent of whether one actually intends to go out and do some hoeing.

What I am trying to do here is to write not from the viewpoint of the practical grower, but for the man who wants to understand what growth is. I am not writing for the professional teacher of mathematics (though teachers may be able to make practical applications of the ideas given here) but for the person who is interested in getting inside the mind of a mathematician.

It is very difficult to communicate the things that are really worth communicating. Suppose, for instance, that you have spent some years in a certain place, and that these years are particularly significant for you. They may have been years of early childhood, or school days, or a period of adult life when new experiences, pleasant or unpleasant, made life unusually interesting. If you revisit this place, you see it in a special way. Your companions, seeing it for the first time, see the physical scene, a pleasant village, a drab town street, whatever it may be. They do not see the essential thing that makes you want to visit the place; to make them see it, you need to be something of a poet; you have to speak of things, but so as to convey what you feel about those things.

But such communication is not impossible. Generally speaking, we overestimate the differences between people. I am sure that if one could go and actually be somebody else for a day, the change would be much less than one anticipated. The feelings would be the same, but hitched on to different objects. Most human misunderstandings are due to the fact that people talk about objects, and forget the varying significance the same object can have for different people.

Generally speaking, teaching conveys thoughts about objects rather than living processes of thought. Suppose someone comes to me with some kind of puzzle; it may be a question in a childs arithmetic book, or a serious problem of scientific research. Perhaps I succeed in solving the puzzle. Then it is quite easy to explain the solution. Suppose I do so; I have shown the questioner how to deal with that particular problem. But if another problem, of a different kind. arises, I shall be consulted again. I have not made my pupil independent of me. What would be really satisfactory would be if I could convey, not simply the knowledge of how to solve a particular puzzle, but the living attitude of mind that would enable my pupil to attack puzzles successfully without help from anyone.

Naturally, there must be certain limitations to what one can expect. Intelligence is one of the factors in problem solving, and it may well be inborn. But there are many other factors - emotions of fear or confidence, habits of self-reliance, initiative, persistence - which depend on education. I do not believe our ancestors at the time of the cave men differed at all from us in inborn qualities of intellect. All historical changes from that time to this, all differences in institutions between one country and another, have essentially been changes in education.

Pelican Books are themselves a symptom of a profound historical change. That there should be in so many different countries of the world a large body of thoughtful men and women reading, studying, forming a kind of invisible, international university - a century ago, or in any previous age one would have looked for such a thing in vain.

At the present time, when our knowledge of material things is so great, and our understanding of ourselves so small, a true appreciation of the enormous unused potentialities of education is essential. The industrial revolution implies and requires a psychological revolution. Psychologically, we still belong to the era when people refused to believe that locomotives would run.

The present book was worked out in a country where a great educational change was taking place. In 1948, the University College of the Gold Coast was founded. The students were keen and of first-rate ability. So far as inborn intelligence went, they were capable of becoming, within ten or twenty years, research workers in mathematics, university lecturers, professors. But of course there was no mathematical tradition in the country. That had to be created.

It was therefore necessary to obtain a sort of essence of mathematics ; to examine the life of a budding mathematician in one of the older mathematical centres; to study all the influences that helped him to grow; the atmosphere of school and college, countless hints, allusions, suggestions from older mathematicians and from books. From all of this to try to form some clear idea of what we were trying to do, what the qualities of a mathematician were, how they were to be stimulated.

In the first five chapters of this book, I try to give a specification of what a mathematician is, and how he grows. These chapters also contain various pieces of mathematics to illustrate what interests a mathematician. The remainder of the book is an exposition of various branches of mathematics; these have been selected for their strangeness, their novelty, their stimulating power. Moreover, they are elementary. A confused recollection of School Certificate mathematics should be sufficient to see a reader through them.

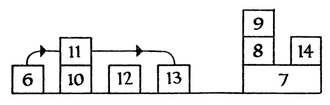
Figure 1 - THE STRUCTURE OF THIS BOOK

Chapters 1-5 use mathematics to illustrate the qualities of a mathematician. They are not shown in the diagram.

Where one chapter is shown as resting on another, the upper chapter makes use of the ideas explained in the lower one. Thus, it is necessary to read Chapter 10 before Chapter 11.

An arrow going from one chapter to another indicates some connexion between the two chapters. For instance, one section of Chapter 13 (the section Finite Geometries) cannot be understood without reference to Chapter 11. But all the rest of Chapter 13 could be read as the first chapter of the book.

It will be seen that bungalows rather than skyscrapers predominate.

Calculus is referred to once or twice, but is nowhere used as part of the argument. This fact is interesting, as showing that some parts of recent mathematics (i.e. since 1800) are not a development of the older work, but have gone off in quite a new direction.