Ziauddin Sardar - Introducing Mathematics: A Graphic Guide

Thus, mathematics is the engine that runs our industrial civilization.
It is the language of science, technology and engineering.
It is essential for architecture and design as well as economics and medicine.
Even art relies on mathematics to some extent.

Indeed, mathematics has become a guide to the world in which we live, the world which we shape and change, and of which we are a part. And as the world becomes more and more complex, and uncertainties in our environment become more urgent and threatening, we need mathematics to describe the risks we face and to plan our remedies.

The ability to deal with mathematics does require a special talent and skill like any other field of human endeavour, such as dancing. Just as an accomplished ballet performance is sophisticated and exquisite, so is mathematics in its essence very elegant and beautiful.

But even though most of us cannot become fully-fledged ballet performers, all of us know what it is to dance and virtually all of us can dance. Similarly, all of us should know what mathematics is about, and be able to understand and handle certain basic steps.

Fear of maths is like of dancing.
Both are overcome by a little bit of practice.

Music is the pleasure the human soul experiences from counting without being aware that it is counting.

C OUNTING

To some extent, young beginners at mathematics retrace the steps of humanity in the development of mathematical knowledge.

At school, children learn to count, to calculate, and to measure. Once they have been learned, these techniques may seem elementary. But for the learners they are full of mystery.

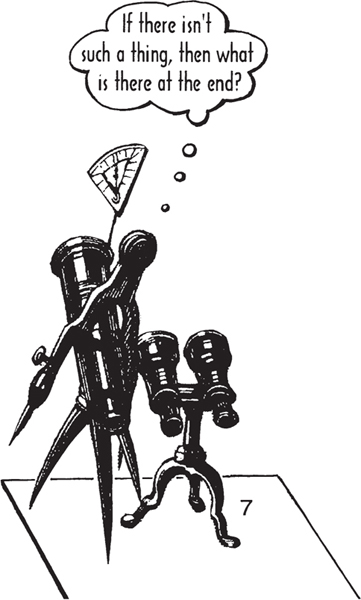
The naming of numbers becomes an incantation, especially when we get to the bigger ones. Counting to a hundred becomes tedious, but getting to a thousand is like climbing a mountain! What is the last number, the biggest one of all?

If there isnt such a thing, then what is there at the end?

How do we name the numbers, as we call them out one after another? Perhaps just a few numbers are enough. Some animals can recognize different collections up to five or seven beyond that its just many. But if we know that numbers go on continuously, we cant just keep inventing new names indefinitely as we go along.

The language of the Dakota Indians was not written down.

So we counted the years and marked special events in our history by keeping a winter count like this one.

It is made of cloth and the pictographs are drawn in black ink. Each year a new pictograph was added to show the main event of the past year.

The best way to systematize naming and counting is to have a base, a number that marks the beginning of counting again. The simplest base is just two. For example, the Gumulgal, an Australian indigenous people, counted like this:

1 = urapon

2 = ukasar

3 = urapon-ukasar

4 = ukasar-ukasar

5 = ukasar-ukasar-urapon

This may seem primitive and tedious.
But the base two, in the form of 0s and 1s ...
...is built into digital computers as the foundation of all their calculations.

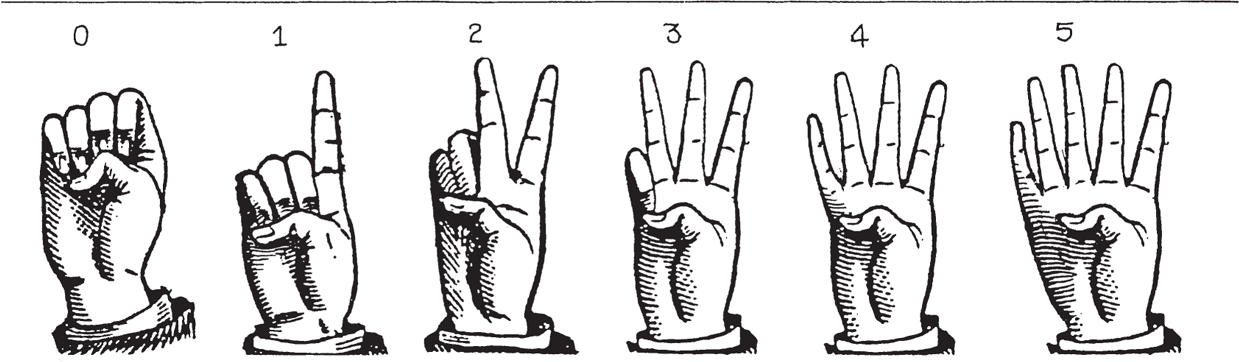
The fingers of the hands are useful for defining bases. Some systems use five, more common is ten. But many other bases can be used. The old British currency had several: twelve (pence per shilling) and then twenty (shillings per pound) and even twenty-one (shillings per guinea!). Shop assistants needed to keep reckoning books by their sides. And when people bought in instalments, they might be told that their living-room suite cost 155 guineas, or 104 weekly payments of one pound, fifteen shillings and sevenpence-halfpenny.

Who could calculate the interest on that?
Small wonder that instalment payments were called the never-never
you never finish paying!

The base twenty (fingers and toes?) is also common. The Yoruba used this, employing subtraction for the larger numbers within the base. They had different names for the numbers one