1. Introduction
The trust in intuitively obvious axioms was destroyed after the discovery of paradoxes in naive set theory at the beginning of the twentieth century. Intuitions dealing with actual infinity, especially, turned out to be misleading and it was necessary to deal with them in a more careful way. On the one hand, Brouwers intuitionism regards mathematics as a languageless, constructive, mental activity and intuitions of the idealized mind should reflect on which constructions are allowed. On the other hand, formalism uses axiomatic systems for mathematical investigations, but tries to eliminate all intuitions form them. This is possible in the way that all meanings are removed from an axiomatic system except for such meanings that can be defined according to the rules of the system itself. The system should be examined regardless of its interpretation. The German mathematician David Hilbert is considered to be the major proponent of formalism. He proposed a research project around 1920, today known as Hilberts program, which was meant as an answer to the crisis brought on by the paradoxes in naive set theory. He aimed to establish secure foundations for all mathematics by grounding all theories on a finite set of axioms and schemata whose consistency should have been proved by finitistic methods. These methods were regarded as reliable and the consistency of the classical mathematics proved with the help of these methods would have provided a justification for non-intuitive parts of the field, especially the parts dealing with actual infinity.
In general, consistency proofs are classified into two groups: absolute and relative consistency proofs. Whereas an absolute consistency proof does not presuppose the consistency of some other system, a relative consistency proof reduces the consistency of a theory
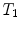
to the consistency of another theory
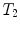
. Thus, we demand a consistency proof for
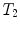
. In this way, we can obtain a potentially infinite hierarchy of theories. Anyway, we need a theory at the beginning of this hierarchy whose consistency can by proved without any reference to another theory, in other words, a theory which has an absolute consistency proof. It seemed that arithmetic is so fundamental that its consistency might be proved within the finitistic methods. This would suffice to regard it as an absolute consistency proof. In late 1930, Gdels incompleteness theorems became known and it was clear that even the tools of arithmetic itself would not suffice to obtain its consistency.
Gerhard Gentzen was a student of Paul Bernays. In early 1932, he set out to work on the consistency of arithmetic. The role of Bernays in this decision of his is not known, but as Gentzen wrote in a letter to Professor Hellmuth Kneser in December 1932 (Menzler-Trott , p. 315):
The axioms of arithmetic are obviously correct, and the principles of proof obviously preserve correctness. Why cannot one simply conclude consistency, i.e., what is the true meaning of the second incompleteness theorem, the one by which the consistency of arithmetic cannot be proved by arithmetic means? Where is the Gdel-point hiding?
In contrast to his predecessors (Frege, Russell), Gentzen was not looking for absolute mathematical truth. He focused on how mathematical theorems are proved in practice, i.e., how one derives a conclusion from given assumptions. The first step he made was that he put aside prevailing proof systems of logicism whose linear derivations did not fit in with the idea of actual mathematical proofs because their starting points were basic logical truths and rules of inference just generated further truths. Gentzens examination of actual reasoning ended in natural deduction calculus whose derivations were in the form of trees. He was probably inspired by Paul Hertz (), whose work he had been studied at the suggestion of Bernays in 1931, when he came up with the tree derivations. Although the tree derivations are in fact a departure form actual proofs, they have some technical advantages over the linear derivations: One can permute the order of rules and compose different derivations without losing a full control over the structure of the result.
The following plan is in Gentzens handwritten thesis manuscript (von Plato , p. 336):
I.
To put up the calculus of natural deduction.
II.
To prove that it is equivalent to standard axiomatic calculi.
III.
To prove that classical arithmetic reduces to intuitionistic arithmetic.
IV.
To prove normalization.
V.
To extend normalization and the subformula property to arithmetic.
Let us explain the items:
I.
The calculi of natural deduction,
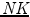
for classical and
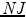
for intuitionistic logic, were completed by September 1932. There are several possibilities which might have led Gentzen to the rules of these calculi. It is known that Gentzen studied Heytings formalization of intuitionistic logic (Heyting , p. 322). His natural deduction calculus originally contained an induction rule. It means that Gentzen was definitely interested in arithmetic.
II.
Gentzen translated derivations in natural deduction into the axiomatic logical calculus of Hilbert and Ackermanns book (Hilbert and Ackermann ) and back.
III.
The third task was accomplished by the Gdel-Gentzen translation which was almost simultaneously developed by both mathematicians after whom it is called. The translation embeds classical arithmetic into intuitionistic one. The result is that it suffices to prove the consistency of intuitionistic arithmetic which would assure that classical arithmetic is consistent, too. We will see that Gentzens plan failed in the item V., so he submitted this result as a separate article to the Mathematische Annalen in March 1933. Then he withdrew the paper because the same result by Gdel ().











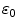 can be formalized in arithmetic, it cannot be proved there. Further, this chapter deals with non-technical parts of his 1936 article.
can be formalized in arithmetic, it cannot be proved there. Further, this chapter deals with non-technical parts of his 1936 article.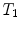 to the consistency of another theory
to the consistency of another theory 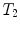 . Thus, we demand a consistency proof for
. Thus, we demand a consistency proof for 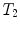 . In this way, we can obtain a potentially infinite hierarchy of theories. Anyway, we need a theory at the beginning of this hierarchy whose consistency can by proved without any reference to another theory, in other words, a theory which has an absolute consistency proof. It seemed that arithmetic is so fundamental that its consistency might be proved within the finitistic methods. This would suffice to regard it as an absolute consistency proof. In late 1930, Gdels incompleteness theorems became known and it was clear that even the tools of arithmetic itself would not suffice to obtain its consistency.
. In this way, we can obtain a potentially infinite hierarchy of theories. Anyway, we need a theory at the beginning of this hierarchy whose consistency can by proved without any reference to another theory, in other words, a theory which has an absolute consistency proof. It seemed that arithmetic is so fundamental that its consistency might be proved within the finitistic methods. This would suffice to regard it as an absolute consistency proof. In late 1930, Gdels incompleteness theorems became known and it was clear that even the tools of arithmetic itself would not suffice to obtain its consistency.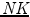 for classical and
for classical and 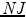 for intuitionistic logic, were completed by September 1932. There are several possibilities which might have led Gentzen to the rules of these calculi. It is known that Gentzen studied Heytings formalization of intuitionistic logic (Heyting , p. 322). His natural deduction calculus originally contained an induction rule. It means that Gentzen was definitely interested in arithmetic.
for intuitionistic logic, were completed by September 1932. There are several possibilities which might have led Gentzen to the rules of these calculi. It is known that Gentzen studied Heytings formalization of intuitionistic logic (Heyting , p. 322). His natural deduction calculus originally contained an induction rule. It means that Gentzen was definitely interested in arithmetic.