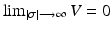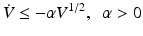Springer Science+Business Media New York 2014
Yuri Shtessel , Christopher Edwards , Leonid Fridman and Arie Levant Sliding Mode Control and Observation Control Engineering 10.1007/978-0-8176-4893-0_1
1. Introduction: Intuitive Theory of Sliding Mode Control
In the formulation of any practical control problem, there will always be a discrepancy between the actual plant and its mathematical model used for the controller design. These discrepancies (or mismatches) arise from unknown external disturbances, plant parameters, and parasitic/unmodeled dynamics. Designing control laws that provide the desired performance to the closed-loop system in the presence of these disturbances/uncertainties is a very challenging task for a control engineer. This has led to intense interest in the development of the so-called robust control methods which are supposed to solve this problem. One particular approach to robust controller design is the so-called sliding mode control technique.
In , the main concepts of sliding mode control will be introduced in an intuitive fashion, requiring only a basic knowledge of control systems. The sliding mode control design techniques are demonstrated on tutorial examples and via graphical exposition. Advanced sliding mode concepts, including sliding mode observers/differentiators and second-order sliding mode control, are studied at a tutorial level. The main advantages of sliding mode control, including robustness, finite-time convergence, and reduced-order compensated dynamics, are demonstrated on numerous examples and simulation plots.
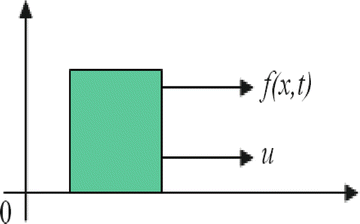
For illustration purposes, the single-dimensional motion of a unit mass (Fig. ) is considered. A state-variable description is easily obtained by introducing variables for the position and the velocity
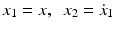
so that
where u is the control force, and the disturbance term f ( x 1, x 2, t ), which may comprise dry and viscous friction as well as any other unknown resistance forces, is assumed to be bounded, i.e., f ( x 1, x 2, t ) L > 0. The problem is to design a feedback control law u = u ( x 1, x 2) that drives the mass to the origin asymptotically. In other words, the control u = u ( x 1, x 2) is supposed to drive the state variables to zero: i.e.,
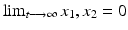
. This apparently simple control problem is a challenging one, since asymptotic convergence is to be achieved in the presence of the unknown bounded disturbance f ( x 1, x 2, t ). For instance, a linear state-feedback control law
provides asymptotic stability of the origin only for f ( x 1, x 2, t ) 0 and typically only drives the states to a bounded domain ( k 1, k 2, L ) for f ( x 1, x 2, t ) L > 0.
Fig. 1.1
Single-dimensional motion of a unit mass
Example 1.1.
The results of the simulation of the system in Eqs. (.
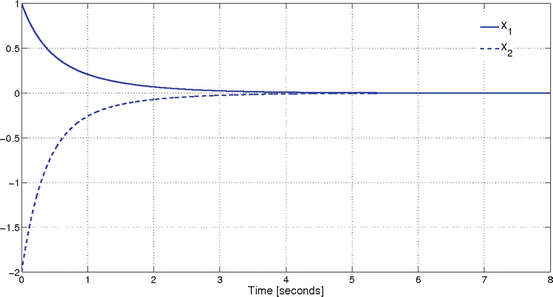
Fig. 1.2
Asymptotic convergence for f ( x 1, x 2, t ) 0
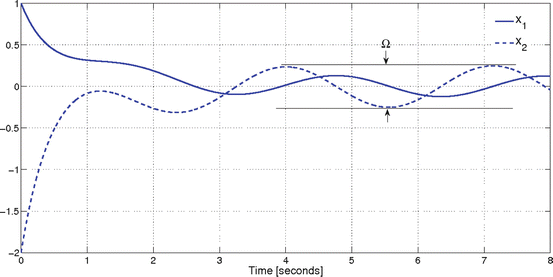
Fig. 1.3
Convergence to the domain for f ( x 1, x 2, t ) = sin(2 t )
The question is whether the formulated control problem can be addressed using only knowledge of the bounds on the unknown disturbance.
1.1 Main Concepts of Sliding Mode Control
Let us introduce desired compensated dynamics for system (). A good candidate for these dynamics is the homogeneous linear time-invariant differential equation:
Since
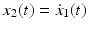
, a general solution of Eq. () and its derivative is given by
both x 1( t ) and x 2( t ) converge to zero asymptotically. Note, no effect of the disturbance f ( x 1, x 2, t ) on the state compensated dynamics is observed. How could these compensated dynamics be achieved? First, we introduce a new variable in the state space of the system in Eq. ():
In order to achieve asymptotic convergence of the state variables x 1, x 2 to zero, i.e.,
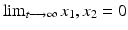
, with a given convergence rate as in Eq. ():
For the -dynamics () a candidate Lyapunov function (see Appendix D) is introduced taking the form
In order to provide the asymptotic stability of Eq. () about the equilibrium point = 0, the following conditions must be satisfied:
(a)
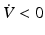
for 0
Condition (b) is obviously satisfied by V in Eq. (). In order to achieve finite-time convergence (global finite-time stability), condition (a) can be modified to be













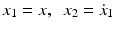 so that
so that 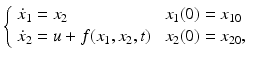
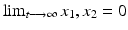 . This apparently simple control problem is a challenging one, since asymptotic convergence is to be achieved in the presence of the unknown bounded disturbance f ( x 1, x 2, t ). For instance, a linear state-feedback control law
. This apparently simple control problem is a challenging one, since asymptotic convergence is to be achieved in the presence of the unknown bounded disturbance f ( x 1, x 2, t ). For instance, a linear state-feedback control law 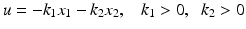
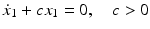
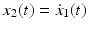 , a general solution of Eq. () and its derivative is given by
, a general solution of Eq. () and its derivative is given by 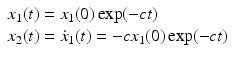
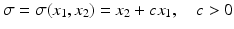
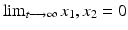 , with a given convergence rate as in Eq. ():
, with a given convergence rate as in Eq. (): 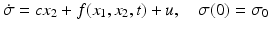
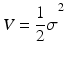
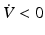 for 0
for 0