Qiskit Pocket Guide
by James L. Weaver
Copyright 2021 James Weaver. All rights reserved.
Printed in the United States of America.
Published by OReilly Media, Inc. , 1005 Gravenstein Highway North, Sebastopol, CA 95472.
OReilly books may be purchased for educational, business, or sales promotional use. Online editions are also available for most titles (http://oreilly.com). For more information, contact our corporate/institutional sales department: 800-998-9938 or corporate@oreilly.com .
- Acquisitions Editor: Suzanne McQuade
- Development Editor: Shira Evans
- Production Editor: Daniel Elfanbaum
- Interior Designer: David Futato
- Cover Designer: Karen Montgomery
- Illustrator: Kate Dullea
- November 2022: First Edition
Revision History for the Early Release
- 2021-08-13: First Release
See http://oreilly.com/catalog/errata.csp?isbn=9781098112479 for release details.
The OReilly logo is a registered trademark of OReilly Media, Inc. Qiskit Pocket Guide, the cover image, and related trade dress are trademarks of OReilly Media, Inc.
The views expressed in this work are those of the author, and do not represent the publishers views. While the publisher and the author have used good faith efforts to ensure that the information and instructions contained in this work are accurate, the publisher and the author disclaim all responsibility for errors or omissions, including without limitation responsibility for damages resulting from the use of or reliance on this work. Use of the information and instructions contained in this work is at your own risk. If any code samples or other technology this work contains or describes is subject to open source licenses or the intellectual property rights of others, it is your responsibility to ensure that your use thereof complies with such licenses and/or rights.
978-1-098-11240-0
[LSI]
Chapter 1. Quantum Circuits and Operations
A Note for Early Release Readers
With Early Release ebooks, you get books in their earliest formthe authors raw and unedited content as they writeso you can take advantage of these technologies long before the official release of these titles.
This will be the 1st chapter of the final book. Please note that the GitHub repo will be made active later on.
If you have comments about how we might improve the content and/or examples in this book, or if you notice missing material within this chapter, please reach out to the editor at .
In Qiskit, quantum programs are normally expressed by placing quantum operations on quantum circuits. Quantum circuits are represented by the QuantumCircuit class, and quantum operations are represented by subclasses of the Instruction class.
Constructing Quantum Circuits
A quantum circuit may be created by supplying an argument that indicates the number of desired quantum wires for that circuit. This is often supplied as an integer:
QuantumCircuit(2)Optionally, the number of desired classical wires may also be specified:
QuantumCircuit(2,2)The number of desired quantum and classical wires may also be expressed by supplying instances of QuantumRegister and ClassicalRegister as arguments to QuantumCircuit. These classes are addressed in .
Using the QuantumCircuit Class
The QuantumCircuit class contains a large number of methods and attributes. The purpose of many of its methods is to apply quantum operations to a quantum circuit. Most of its other methods and attributes either manipulate, or report information about, a quantum circuit.
Commonly used gates
contains some commonly used single-qubit gates and code examples. Variable qc refers to an instance of QuantumCircuit that contains at least four quantum wires:
Table 1-1. Commonly used single-qubit gates in Qiskit
| Names | Example | Notes |
|---|
H, Hadamard | qc.h(0)
| Applies H gate to qubit 0. See . |
I, Identity | qc.id(2) or qc.i(2)
| Applies I gate to qubit 2. See . |
P, Phase | qc.p(math.pi/2,0)
| Applies P gate with /2 phase rotation to qubit 0. See . |
RX | qc.rx(math.pi/4,2)
| Applies RX gate with /4 rotation to qubit 2. See . |
RY | qc.ry(math.pi/8,0)
| Applies RY gate with /8 rotation to qubit 0. See . |
RZ | qc.rz(math.pi/2,1)
| Applies RZ gate with /2 rotation to qubit 1. See . |
S | qc.s(3)
| Applies S gate to qubit 3. Equivalent to P gate with /2 phase rotation. See . |
S | qc.sdg(3)
| Applies S gate to qubit 3. Equivalent to P gate with 3/2 phase rotation. See . |
SX | qc.sx(2)
| Applies SX (square root of X) gate to qubit 2. This is equivalent to an RX gate with a /2 rotation. See . |
T | qc.t(1)
| Applies T gate to qubit 1. Equivalent to P gate with /4 phase rotation. See . |
T | qc.tdg(1)
| Applies T gate to qubit 1. Equivalent to P gate with 7/4 phase rotation. See . |
U | qc.u(math.pi/2,0,math.pi,1)
| Applies rotation with 3 Euler angles to qubit 1. See . |
X, NOT | qc.x(3)
| Applies X gate to qubit 3. See . |
Y | qc.y([0,2,3])
| Applies Y gates to qubits 0, 2 and 3. See . |
Z | qc.z(2)
| Applies Z gate to qubit 2. Equivalent to P gate with phase rotation. See . |
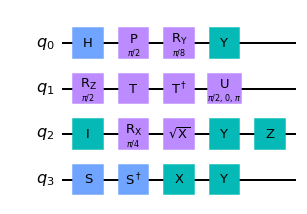
Figure 1-1. Nonsensical circuit with single-qubit gate examples
contains some commonly used multi-qubit gates and code examples. Variable qc refers to an instance of QuantumCircuit that contains at least four quantum wires:
Table 1-2. Commonly used multi-qubit gates in Qiskit
| Names | Example | Notes |
|---|
CCX, Toffoli | qc.ccx(0,1,2)
| Applies the X gate to quantum wire 2, subject to the state of the control qubits on wires 0 and 1. See . |
CH | qc.ch(0,1)
| Applies the H gate to quantum wire 1, subject to the state of the control qubit on wire 0. See . |














