1.1 Background
In todays modern age, an enormous amount of neural data have been recorded or collected (Stevenson and Kording ). It remains a great challenge to process and analyze this big data. By nature, neural signals are stochastic (noisy) signals measured from dynamic processes in the brain at various spatiotemporal scales. The term dynamic is emphasized because the neural signals are generated from biophysical processes (i.e., neurons) that have memory. Neural signals are often modeled as non-stationary stochastic processes. Unlike other physical signals, neural signals are driven by complex behaviors of experimental subjects. In some cases, multi-modal neural data are simultaneously collected at different spatial and temporal scales. The development of efficient quantitative methods to characterize these recordings and extract information that reveals underlying neurophysiological mechanisms remains an active and important research field.
To date we have witnessed tremendous advances and growing interests in applying statistics, signal processing, control and modeling methods to neuroscience. Meanwhile, new applications encounter emerging problems and challenges. Therefore, it is important to recognize these challenges and frequently exchange innovative ideas among researchers at both computational and experimental ends as well as those at the interface. We will review some important research topics and progresses of applying quantitative methods for neuroscience data. The concept of dynamics is emphasized throughout the book.
1.2 Statistics and Signal Processing in Neuroscience
Analysis of neurophysiological or behavioral data from neuroscience investigations is a fundamental task in computational and statistical neuroscience (Brown et al. ). The task can be challenging when the following one or more scenarios are present: (i) The dimensionality of the data is scaled up from an order of tens to hundreds or even larger; (ii) The data are either super noisy with a very low signal-to-noise (SNR) ratio or large variability (across trials or time); (iii) The exact quantitative mapping between neural codes and the measured behavior is always partially unknown, given partial observations of behavioral measures and neural recordings.
The core of statistics is data science. The data are generated and collected from neuroscience experiments at neurophysiological, imaging, or behavioral levels. In their article What is statistics published in American Statistician , Brown and Kass defined two fundamental principles for statistical thinking (Brown and Kass ):
Statistical models of regularity and variability may be used to express knowledge and uncertainty about a signal in the presence of noise, via inductive reasoning.
Statistical methods may be analyzed to determine how well they are likely to perform.
The first principle focuses on the construction of statistical models, whereas the second principle focuses on the evaluation of statistical inference procedures. Depending on the model assumption, statistical models can be parametric, semiparametric , or nonparametric , with a trend in growing model complexity. It is important to stress the motto: all models are wrong, but some are useful, in a sense that statistical models need to be adapted or modified according to the need, which may or may not fully reflect the truth of data generating process.
Based on these two principles, likelihood or Bayesian methods can be developed for neural data analysis (Pawitan .
Table 1.1
Examples of statistical models and inference
| Likelihood inference | Bayesian inference |
|---|
Parametric | Linear regression, GLM | Particle filter (Doucet et al. ) |
Semiparametric | Finite mixture models | BARS (DiMatteo et al. ) |
Nonparametric | KDE, Kernel regression | GP, Dirichlet process mixtures (Hjort et al. ) |
Signal processing is a discipline that encompasses the fundamental theory, applications, algorithms, and implementations of processing or transferring information contained in signals. Roughly speaking, we can classify fundamental tasks of statistical signal processing into three categories: signal recovery (examples of such include a wide range of inverse problems such as filtering, detection, denoising, and deconvolution), representation and visualization (examples of such include spectral analysis, subspace identification, compression), and prediction and control (the problem of control will be addressed separately in the next section). The goal of neural signal processing is to combine statistics, signal processing, and optimization methods to process neural data of diverse sources. Unlike traditional signal processing assumptions, neural signal processing often deals with neurophysiological signals with non-Gaussianity, non-stationarity, and heterogeneity (Chen ). Over the past decades, many statistical signal processing tools have been developed for various neuroscience applications. We will briefly review a few important applications in this area.
1.2.1 Neural Coding
From a neural coding perspective, there are encoding and decoding phases (Fig. c for an example). For instance, in visual systems, the neuronal tuning function is characterized by a 2D spatiotemporal RF; whereas in auditory systems, it is characterized as a spectrotemporal RF (STRF). In the case of auditory neurons, the classic STRF model assumes a linear relationship between the time-dependent neuronal response r ( t k ) and the time-frequency spectrum of acoustic stimuli s ( k , ):
where r 0 denotes the baseline firing rate, s ( k , ) denotes the stimulus energy at different tonotopic locations and different time delays >0. The strength and nature of the influences, whether being excitatory (positive) or suppressive (negative), is described by the STRF gain function STRF (, ). The traditional method for mapping the neuronal RF is reverse correlation (Ringach and Shapley )
where 0 is a constant, h ( l ) is a finite-length post-spike filter, n ( k l ) denotes the spike count in the previous l -th window before time index k , and f () is a static nonlinearity, which can be an exponential:
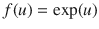
, or
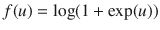
, or a custom function (e.g.,
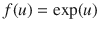

















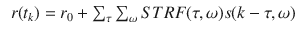
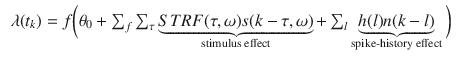
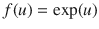 , or
, or 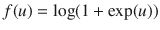 , or a custom function (e.g.,
, or a custom function (e.g.,