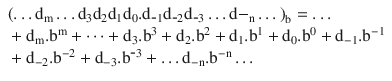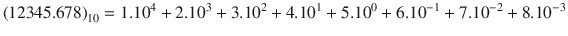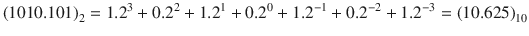Salvador Pinillos Gimenez - 8051 Microcontrollers: Fundamental Concepts, Hardware, Software and Applications in Electronics

8051 Microcontrollers: Fundamental Concepts, Hardware, Software and Applications in Electronics — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "8051 Microcontrollers: Fundamental Concepts, Hardware, Software and Applications in Electronics" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

1234567...80

Springer International Publishing AG, part of Springer Nature 2019

Salvador Pinillos Gimenez 8051 Microcontrollers

1. Fundamental Concepts of Computer Systems

Salvador Pinillos Gimenez 1

(1)

FEI University Center, So Paulo, So Paulo, Brazil

This chapter describes the main basic concepts of computer systems.

1.1 Introduction

The majority of electronics products (cellular phones, tablets, notebooks, radios, smart televisions, etc.) are currently implemented with microprocessors, memories and basic electronic circuits, named input/output interfaces, which perform the interaction with the humans. These basic electronic circuits compose the computer systems. So, this chapter aims to describe the fundamental concepts to understand these wonderful machines.

1.2 Numeral Systems (System of Numeration)

The law of numerical formation in a specific base (b) is given by ... dmd3d2d1d0.d1d2d3d-n ..., where dm and dn represent a specific digit of the considered numerical base, before and after the point, respectively, and m + 1 and n are the quantity of digits that define the number, before and after the point, respectively. In order to know how this number is given in the decimal base, we need to use Eq. ( ].

(1.1)

For instance, if m is equal to 9, the number has 10 digits before the point (integer part of the number), and if n is equal to 5, the number has 5 digits after the point (fractional part of the number). If there are ten digits before the point (d9 d0), the digit d9 is defined as the most significant digit (MSD), and if there are three digits after the point, d3 is defined as the least significant digit (LSD) [].

To exemplify, the number 12345.678 in the base 10 (decimal representation) can be represented by using Eq. ( ]:

(1.2)

In Eq. ( ].

Similarly, the value in the base 10 of the number 1111.01 in the base 2, i.e., (1111.01)2, is given by Eq. ( ]:

(1.3)

The numerical bases that are most commonly used in computer systems are the binary, hexadecimal, and BCD (binary-coded decimal) [].

1.2.1 Decimal Numeral System (Base 10)

It is the numeral system used by humans, which is composed of ten digits, named decimal digits: 0, 1, 2, ..., 9 [].

1.2.2 Binary Numeral System

The binary digits or bits are formed by the digits 0 and 1. They belong to the base 2 numeral system. This numeral system is commonly used in computer systems because it is capable of representing the digital electrical behavior of the transistors operating as a switch, i.e., open switch (cut-off region: deactivated condition, turn-off, etc.) and off switch (triode region: activated condition, turn-on, the transistor is saturated, etc.). Regarding the logic positive in digital electronics, the open-switch condition of the transistor is defined as zero logic or 0 logic and the off-switch condition of the transistor is defined as one logic or 1 logic. The 0 logic usually corresponds to the 0 volt (0 V), and the 1 logic corresponds to the 5.0 volts (5.0 V), 3.0 V, 1.2 V, etc., depending on the complementary metal-oxide semiconductor (CMOS) of integrated circuit (IC) technology adopted [].

The number of binary combinations generated by a bit is equal to 2 (2number of bits = 21 = 2), i.e., there are two possible binary combinations, which can be 0 logic or 1 logic, as illustrated in Table ].

Table 1.1

Number of binary combinations by using a bit

Binary combinations by using a bit	bit	Decimal value
First binary combination		020 = 0
Second binary combination		121 = 1

The highest value of the binary combination that can be represented with one single bit is defined as the number of binary combinations subtracted by one, i.e., 2(number of bits 1) = 211 = 21 = 1, as indicated in Table ].

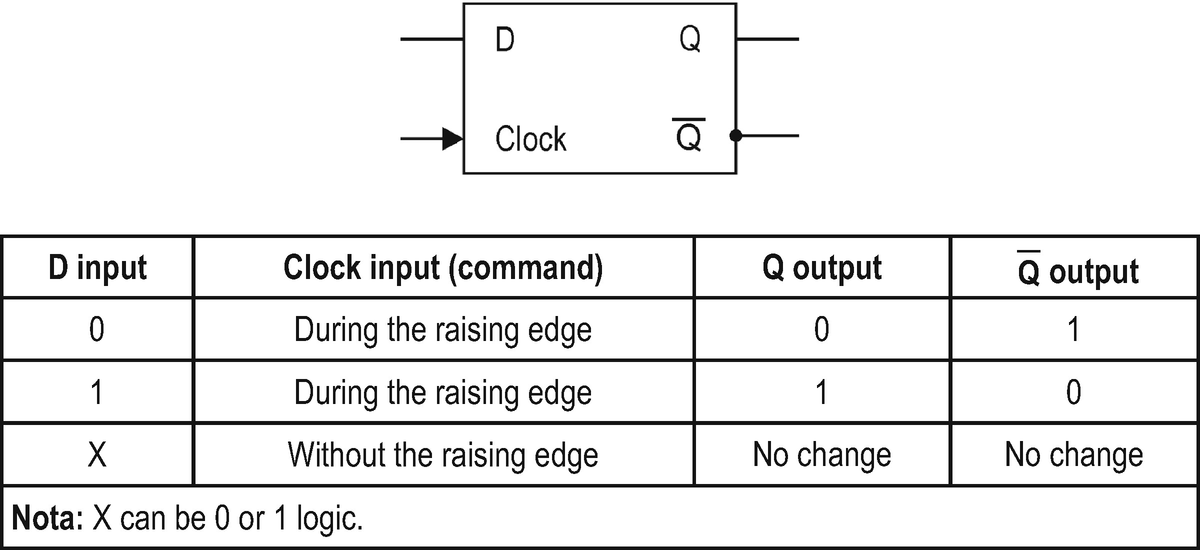
The synchronous D-type flip-flop (with clock input) is an example of a basic digital circuit which is responsible for storing a single bit, according to Fig. ].

Fig. 1.1

Electrical representation of the synchronous D-type flip-flop and its truth table

When a bit is defined in the input of a synchronous D-type flip-flop, it will be only copied and stored in the Q output when a rising edge (from 0 to 1 logic) is set in its clock input. The absence of an electrical signal (rising edge) in the clock input does not enable the copy and storage of the bit from the D input to the Q output, and consequently its Q output remains with the previous state. The minimum time of the clock pulse or the maximum frequency that a synchronous D-type flip-flop can operate is determined by the CMOS ICs technology used. The higher the frequency of the flip-flops, the higher the processing speed of computer systems [].

The numerical representation using 8 bits is defined as a byte. The number of possible binary combinations with 8 bits is 256 (2number of bits = 28), and the highest value of this numerical representation is 255 (2number of bits 1 = 281 = 2561), as shown in Table ].

Table 1.2

Possible binary combinations in an 8-bit binary presentation (byte)

Binary combinations in an 8-bit binary presentation (byte)	Byte D7D6D5D4D3D2D1D0 2726252423222120	Decimal value
First binary combination	0 0 0 0 0 0 0 0	027 + 026 + 025 + 024 + 023 + 022 + 021 + 020 = 0
Second binary combination	0 0 0 0 0 0 0 1	027 + 026 + 025 + 024 + 023 + 022 + 021 + 121 = 1
Third binary combination	0 0 0 0 0 0 1 0	027 + 026 + 025 + 024 + 023 + 022 + 121 + 021 = 2
Fourth binary combination	0 0 0 0 0 0 1 1	027 + 026 + 025 + 024 + 023 + 022 + 121 + 121 = 3
Fifth binary combination	0 0 0 0 0 1 0 0	027 + 026 + 025 + 024 + 023 + 122 + 021 + 021 = 4
Sixth binary combination	0 0 0 0 0 1 0 1	027 + 026 + 025 + 024 + 023 + 122 + 021 + 121 = 5
:	:	:
Penultimate binary combination	1 1 1 1 1 1 1 0	127 + 126 + 125 + 124 + 123 + 122 + 121 + 021 = 254
Last binary combination	1 1 1 1 1 1 1 1	127 + 126 + 125 + 124 + 123 + 122 + 121 + 121 = 255

Next page

1234567...80

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

Similar books «8051 Microcontrollers: Fundamental Concepts, Hardware, Software and Applications in Electronics»

Look at similar books to 8051 Microcontrollers: Fundamental Concepts, Hardware, Software and Applications in Electronics. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.

Ned Mohan

Power Electronics, A First Course: Simulations and Laboratory Implementations

Norman Dunbar

Arduino Software Internals: A Complete Guide to How Your Arduino Language and Hardware Work Together

Charles Bell

Beginning MicroPython with the Raspberry Pi Pico: Build Electronics and IoT Projects

Cem Ünsalan

Embedded System Design with ARM Cortex-M Microcontrollers: Applications with C, C++ and MicroPython

Neil Cameron

Electronics Projects with the ESP8266 and ESP32: Building Web Pages, Applications, and WiFi Enabled Devices

Engr. Michael David

Hand-On Embedded System Architecture : Introduction to Robotics and the AVR Microcontroller Practical Guide For Students and Professionals

Anbazhagan K

8051 Microcontroller Best 10 Projects: RFID Interfacing, Advanced Thermometer, Computerized Clock, Graphical LCD, Advanced Code Lock, PIR Sensor and GSM Based Security, etc.

Donald Norris

Programming with STM32: Getting Started with the Nucleo Board and C/C++

Neil Cameron

Arduino Applied: Comprehensive Projects for Everyday Electronics

Charles Bell

MicroPython for the Internet of Things: A Beginner’s Guide to Programming with Python on Microcontrollers

Elliot Williams

Make: AVR Programming: Learning to Write Software for Hardware

Alan Trevennor

Practical AVR microcontrollers : games, gadgets, and home automation with the microcontroller used in the Arduino

Discussion, reviews of the book 8051 Microcontrollers: Fundamental Concepts, Hardware, Software and Applications in Electronics and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.