Jon Harrop - The OCaml Journal, 2007-2010

1. (8th June 2007)
2. (8th June 2007)
3. (23rd June 2007)
4. (10th July 2007)
5. (24th July 2007)
6. (9th August 2007)
7. (23rd August 2007)
8. (8th September 2007)
9. (24th September 2007)
10. (8th October 2007)
11. (23rd October 2007)
12. (12th November 2007)
13. (23rd November 2007)
14. (12th December 2007)
15. (28th December 2007)
16. (10th January 2008)
17. (24th January 2008)
18. (9th February 2008)
19. (25th February 2008)
20. (8th March 2008)
21. (26th March 2008)
22. (10th April 2008)
23. (25th April 2008)
24. (10th May 2008)
25. (23rd May 2008)
26. (10th June 2008)
27. (22nd June 2008)
28. (10th July 2008)
29. (27th July 2008)
30. (10th August 2008)
31. (27th August 2008)
32. (10th September 2008)
33. (23rd September 2008)
34. (10th October 2008)
35. (23rd October 2008)
36. (10th November 2008)
37. (23rd November 2008)
38. (10th December 2008)
39. (23rd December 2008)
40. (10th January 2009)
41. (23rd January 2009)
42. (10th February 2009)
43. (23rd February 2009)
44. (8th March 2009)
45. (23rd March 2009)
46. (8th April 2009)
47. (23rd April 2009)
48. (8th May 2009)
49. (23rd May 2009)
50. (8th June 2009)
51. (23rd June 2009)
52. (10th July 2009)
53. (23rd July 2009)
54. (8th August 2009)
55. (23rd August 2009)
56. (8th September 2009)
57. (23rd September 2009)
58. (8th October 2009)
59. (23rd October 2009)
60. (8th November 2009)
61. (23rd November 2009)
62. (8th December 2009)
63. (23rd December 2009)
64. (8th January 2010)
65. (23rd January 2010)
66. (8th February 2010)
67. (23rd February 2010)
68. (8th March 2010)
69. (23rd March 2010)
70. (8th April 2010)
71. (23rd April 2010)
72. (8th May 2010)
73. (23rd May 2010)
74. (8th June 2010)
75. (23rd June 2010)
76. (8th July 2010)
77. (23rd July 2010)
78. (8th August 2010)

To receive notifications as new articles are published, please subscribe to our OCaml News blog feed available from this page.

If you are enjoying our articles, please write a review of the OCaml Journal and encourage other people to subscribe!

The A* algorithm is often used for route finding in game AI and is a generalization of Dijkstra's shortest-path algorithm from graph theory. This article describes a simple implementation of the A* algorithm written in OCaml that makes extensive use of the module system including higher-order modules (functors) in order to provide a reusable implementation of this algorithm that is generic over the kinds of graphs that it can handle. Finally, an example application is provided that finds a route around a hill.

Dijkstra's shortest path algorithm finds the shortest path between a pair of nodes in a graph using a breadth-first traversal that incrementally expands a set of nodes around the first node until it includes the second node. Consequently, applying Dijkstra's algorithm to a planar problem results in a roughly circular set of searched nodes. This represents a lot of wasted effort because half of steps taken were in the wrong direction.

In many cases, this naive shortest path algorithm may be substantially improved upon by biasing the search towards nodes that are closer according to some heuristic, such as the Euclidean distance between the nodes. In the simplest case of a flat terrain, this heuristic-based algorithm will find the shortest path almost immediately by taking steps from the first node directly towards the second node. This is the A* algorithm.

This article describes a simple but efficient and reusable implementation of the A* algorithm in OCaml.

In order to abstract our program over the kinds of graphs it can handle, we begin by defining a module signature for a node in a graph that contains the type of each definition required by our algorithm:

# module type NODE = sig
type t
val compare : t -> t -> int
val dist : t -> t -> float
val neighbors : t -> t list
end;;
module type NODE =
sig
type t
val compare : t -> t -> int
val dist : t -> t -> float
val neighbors : t -> t list
end

The type t is the abstract type of a node from the point of view of any functor consuming modules of this NODE signature. The compare function is the conventional total ordering over values of the type t. The dist function computes the distance between two nodes and is exact when the nodes are adjacent. The neighbors function returns the list of neighboring nodes of any given node.

Now we can define our A* algorithm abstractly as an AStar functor that accepts any module implementing the NODE signature:

# module AStar(N: NODE) : sig
val search : N.t -> N.t -> N.t list option
end = struct

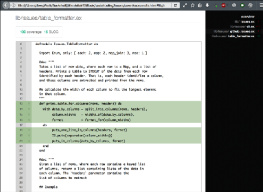
The signature of our functor indicates that it must define a search function that takes a pair of nodes and returns a list including those nodes representing the shortest path between them. An option type is used to convey when no path could be found between the nodes.

Our algorithm will use a functional map from nodes to metadata and sets of nodes. The map is easily implemented by applying the Map.Make functor to the N module that was passed to our AStar functor:

module Map = Map.Make(N)

One of our sets of nodes, the set of open nodes, must be kept sorted by the estimated path length so we define a Meta module that augments N with the necessary metadata and provides a new compare function that sorts nodes first by f (the estimated path length) and then by the node itself (being careful to reuse the N.compare function rather than the built-in polymorphic compare function which may not provide the correct total ordering over nodes):

module Meta = struct
type t = { path: N.t list; g: float; f: float; node: N.t }
let compare n1 n2 =
let c = compare n1.f n2.f in
if c<>0 then c else
N.compare n1.node n2.node
end

The open set is then implemented by applying the Set.Make functor to our Meta module:

module OpenSet = struct
include Set.Make(Meta)
let split_min xs =
let x = min_elt xs in
x, remove x xs
end

As this set is acting as a heap, keeping the nodes sorted by estimated path length, we have augmented it with a split_min function that returns the first node (with the shortest estimated path length) and remaining set.

The closed set requires no such special ordering so it is created simply by applying the Set.Make functor to the N module:

module ClosedSet = Set.Make(N)