
John Napier: Life, Logarithms, and Legacy
John Napier
LIFE, LOGARITHMS, AND LEGACY
Julian Havil
PRINCETON UNIVERSITY PRESS
PRINCETON AND OXFORD
Copyright 2014 by Princeton University Press
Published by Princeton University Press,
41 William Street, Princeton, New Jersey 08540
In the United Kingdom: Princeton University Press,
6 Oxford Street, Woodstock, Oxfordshire OX20 1TW
All Rights Reserved
ISBN: 978-0-691-15570-8 (alk. paper)
Library of Congress Control Number: 2012931844
British Library Cataloguing-in-Publication Data is available
This book has been composed in LucidaBright
Typeset by T&T Productions Ltd, London
Printed on acid-free paper
press.princeton.edu
Printed in the United States of America
1 3 5 7 9 10 8 6 4 2
This book is dedicated to my students who, over many years, have provided the catalyst to perpetuate a teachers enthusiasm
Writing a book is an adventure. To begin with it is a toy, then an amusement. Then it becomes a mistress, and then it becomes a master, and then it becomes a tyrant and, in the last stage, just as you are about to be reconciled to your servitude, you kill the monster and fling him to the public.
Churchill, Churchill By Himself
Richard Rich: And if I was (a good teacher), who would know it?
Sir Thomas More: You, your pupils, your friends, God. Not a bad public, that
Robert Bolt, A Man For All Seasons
I think and I think for months and years. Ninety-nine times, the conclusion is false. The hundredth time I am right.
Einstein
John (whom we now call Napier, but who never spelt his name that way in his life) actually spelt his name FIVE different ways on one page of a letter
Charlie Napier

The Napiers are believed to be descendants of the Celtic earldom of Lennox and there is a close similarity between the Napier and Lennox coats of arms. The name itself is almost certainly derived from the term Napper, the Keeper of the Linen in a royal or lordly household.
Ancestral Scotland
Contents
Acknowledgments
I should like to record my thanks to and admiration of my editor, Vickie Kearn, and gratitude to all those at Princeton University Press who have helped in their many ways to ensure the books completion. I am also grateful to the anonymous reviewers for their comments and suggestions: I hope that they feel I have listened sufficiently to them. Jon Wainwright of T&T Productions Ltd has yet again set the standard for typesetting, both with his evident expertise but also with his accommodating manner: nothing was too much trouble for him. Where my Latin failed me, I have relied on various older translations but also, particularly, on the work of Ian Bruce of http://www.17centurymaths.com/, which is a marvellous initiative. Lastly, I acknowledge the inevitable existence of what John Napier termed slippery errors, for which I apologize: if only perception and reality were the same thing.
Introduction
Glory is fleeting, but obscurity is forever.
Napoleon Bonaparte
On 16 February 2012 the British prime minister, David Cameron, gave a speech in Scotlands capital of Edinburgh on a theme that would have had resonance with John Napier: sieges, alliances and intrigues that have absorbed the country, the prime minister was on safe ground with his opening sentence:
The air in Scotland hangs heavy with history.
His second sentence
Edinburghs cityscape is studded with monuments to memories.
brings us, though, to a motivation for this book: a monument of significance is missing. The speechwriters had combed through that long history to find the names of Scotsmen whose contribution in whatever field has been of significance. This was not a difficult task and, as we comb through their speech, we find, in order of mention: Walter Scott, Robert Louis Stevenson, John Knox, Captain Scott, Adam Smith, David Hume, James Maxton, Keir Hardie, John Reith, Lord Lovat, Robert Dunsire, Liam Tasker, James Watt, Robert Owen, Sir Bill Gammell, Ian
Here I stand at what is called the Cross of Edinburgh, and can, in a few minutes, take 50 men of genius and learning by the hand.
In short, Scottish history is enviably replete with names of significance, but that of the Edinburgh born John Napier is in danger, if not of disappearing from the scientific landscape, then of fading into its shadows. His name is now seldom attached to the logarithms he (in essence) discovered, with the modern nomenclature of Natural replacing Naperian logarithm. In an online poll conducted by the National Library of Scotland between December 2005 and October 2006, the public were invited to vote for a favourite Scottish scientist out of 24 nominees, Napier was one of them and appeared last of the subsequently published top 10; or any other prior intellectual, it is simply that Napier was in modern terms a research mathematician of exceptional power, although one working with crude tools. In Scotland he was succeeded by more of Amyatts men of genius, beginning with James Gregory, James Sterling and Colin Maclaurin; in England the long list of such begins with Henry Briggs, his irreplaceable collaborator in the development of logarithms.
With our (not so very) modern view of logarithms it may be difficult at first to appreciate that they needed inventing; for us they are, after all, simply the inverse of the exponential functions, with the problem merely one of notation:
If y = x2 then 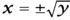 , but if y = 2x, then how do we write x?
, but if y = 2x, then how do we write x?
We must thank the Silesian mathematician Christoff Rudolff for the radical sign; the answer to the second question, known to all high-school mathematics students, is of course x = log2y; the instructor is left with the motivational difficulty of why a lump of wood enters mathematical notation. Yet, the problem is also a calculative one: the solution to the equation 2x = 4 is far removed in difficulty from that of 2x = 3; this latter equation would have us reaching for the calculator button which provides logarithms to any base or the ones labelled log and ln. Of these last two, the former produces what is now a logarithm of convenience and the latter one of essence and it is in the distinction between them that there lies concealed a nice logarithmic paradox. It is that base 10 logarithm, log, which was to bring to a world desperate for calculative help a mechanism, realized as a table of numbers, which conjured the immensely challenging problem of multiplication to the comparatively simpler one of addition. The younger reader, who rightly takes for granted modern calculative tools, should beware complacency: we do not doubt that the product 742849628465 269355497183 would, with time and great care, be correctly accomplished by hand but now let this problem be one of a hundred such, a thousand such, , and we begin to comprehend the immense calculative difficulties faced by and we may imagine ourselves dealing with a trigonometric calculation of great accuracy, as they routinely did; perhaps it arose from a problem in positional astronomy with the use of the sine rule or the cosine rule or one of numerous other such rules, all of which they had. But it is one thing to find a numeric expression for an unknown quantity: it is quite another to evaluate that expression. These then, in tabular form, are the logarithms that were in use for calculation up to the mid 1970s (and, in many places, still later) but, if the single purpose of logarithms was their original purpose, to aid calculation, their place would now be solely the remit of the mathematical historian yet, even though the tables of logarithms have disappeared, logarithms themselves remain an essential current mathematical tool: measurement of sound levels, earthquake intensity, pH levels, entropy, stimulus and sensation response, etc., hardly touches the number of real-world phenomena which exhibit logarithmic behaviour. With these and their like the choice of base is not a critical matter, but it is with base e, or ln, that logarithms are most notably imbued with their immortality: where would calculus be without ln
Next page
















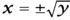 , but if y = 2x, then how do we write x?
, but if y = 2x, then how do we write x?