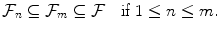Part 1
An Introductory Course in Stochastic Processes
Stphane Crpey Springer Finance Financial Modeling 2013 A Backward Stochastic Differential Equations Perspective 10.1007/978-3-642-37113-4_1 Springer-Verlag Berlin Heidelberg 2013
1. Some Classes of Discrete-Time Stochastic Processes
Stphane Crpey 1
(1)
Dpartement de mathmatiques, Laboratoire Analyse & Probabilits, Universit dEvry Val dEssone, Evry, France
Abstract
The most important mathematical tools in pricing and hedging applications are certainly martingale and Markov properties. Martingality can be stated as a stochastic equation written in terms of conditional expectations. The Markov property can be stated in terms of deterministic semi-group Kolmogorov equations. The tower rule for conditional expectations and Markovian semi-group equations can be considered as primary dynamic programming pricing equations, in their stochastic and deterministic form (to mature as stochastic pricing BSDEs and deterministic pricing PIDEs later in the book). Practically speaking, a Markov property is a necessary companion to a martingale condition in order to ensure tractability (up to the curse of dimensionality). From an opposite perspective, martingales can be used to pursue some theoretical developments beyond a Markov setup. Its interesting to note that historically, stochastic calculus was first developed as a tool for the study of Markov processes, until it was realized that the theory of martingales, in particular, was interesting for its own sake, allowing one to supersede Markovianity.
To emphasize these fundamental ideas at the simplest possible level of technicality, we present them in this first chapter in discrete time. We start with the definition and main properties of conditional expectation. The former is in fact mainly useful to prove the latter (which we leave to standard probability textbooks), since most practical conditional expectation computations are directly based on these properties, with the tower rule as a most emblematic example. We then introduce discrete time Markov chains and martingales in this spirit and with finance already in mindbasing most of our examples on random walks fortune processes, like with the doubling strategy, which grants a wealth of one for sure in the end but with values that are unbounded from below on the way!
1.1 Discrete-Time Stochastic Processes
1.1.1 Conditional Expectations and Filtrations
We first discuss the notions of conditional expectations and filtrations which are key to the study of stochastic processes.
Definition 1.1.1
Let and 1,, n be random variables. The conditional expectation
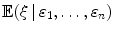
is a random variable characterized by two properties.
(i)
The value of
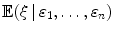
depends only on the values of 1,, n , i.e. we can write
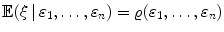
for some function . If a random variable can be written as a function of 1,, n , it is said to be measurable with respect to 1,, n .
(ii)
Suppose
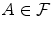
is any event that depends only on 1,, n . Let
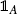
denote the indicator function of A , i.e. the random variable which equals 1 if A occurs and 0 otherwise. Then
As a random variable,
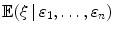
is a function of . Thus, the quantity
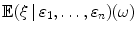
is a value of
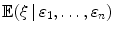
. Sometimes a less formal, but more convenient notation is used: suppose is such that i ()= x i , i =1,, n . Then, the notation
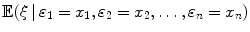
is used in place of
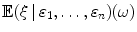
. Likewise, for the value of the indicator random variable
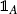
, where
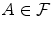
, the notation
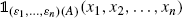
is used instead of
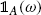
, with the understanding that ( 1,, n )( A )={( 1(), 2(),, n ()), A }.
Example 1.1.2
We illustrate the equality () with an example in which n =1. Suppose that and are discrete random variables and A is an event which involves . (For concreteness we may think of as the value of the first roll and as the sum of the first and second rolls in two rolls of a dice, and A ={2}). We have, using the Bayes formula in the fourth line:
For the example involving dice, taking ( A )={ x 2}
and
It will be convenient to make the notation more compact. If 1, 2, is a sequence of random variables we will use
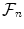
to denote the information contained in 1,, n , and we will write
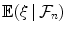
for
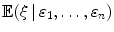
.










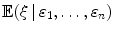 is a random variable characterized by two properties.
is a random variable characterized by two properties. 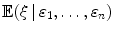 depends only on the values of 1,, n , i.e. we can write
depends only on the values of 1,, n , i.e. we can write 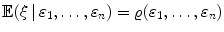 for some function . If a random variable can be written as a function of 1,, n , it is said to be measurable with respect to 1,, n .
for some function . If a random variable can be written as a function of 1,, n , it is said to be measurable with respect to 1,, n .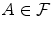 is any event that depends only on 1,, n . Let
is any event that depends only on 1,, n . Let 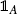 denote the indicator function of A , i.e. the random variable which equals 1 if A occurs and 0 otherwise. Then
denote the indicator function of A , i.e. the random variable which equals 1 if A occurs and 0 otherwise. Then 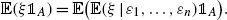
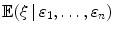 is a function of . Thus, the quantity
is a function of . Thus, the quantity 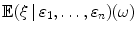 is a value of
is a value of 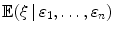 . Sometimes a less formal, but more convenient notation is used: suppose is such that i ()= x i , i =1,, n . Then, the notation
. Sometimes a less formal, but more convenient notation is used: suppose is such that i ()= x i , i =1,, n . Then, the notation 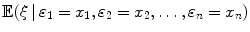 is used in place of
is used in place of 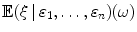 . Likewise, for the value of the indicator random variable
. Likewise, for the value of the indicator random variable 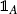 , where
, where 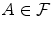 , the notation
, the notation 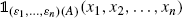 is used instead of
is used instead of 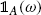 , with the understanding that ( 1,, n )( A )={( 1(), 2(),, n ()), A }.
, with the understanding that ( 1,, n )( A )={( 1(), 2(),, n ()), A }.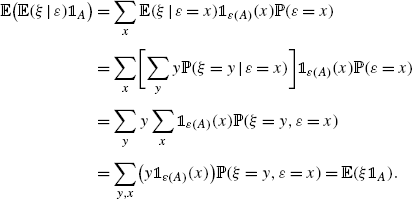
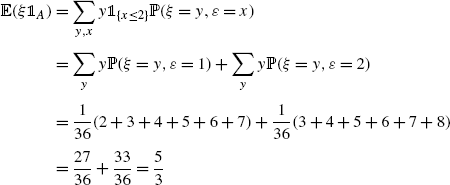
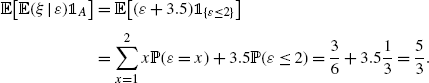
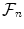 to denote the information contained in 1,, n , and we will write
to denote the information contained in 1,, n , and we will write 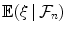 for
for 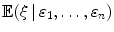 .
.