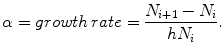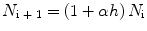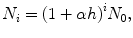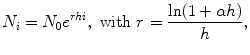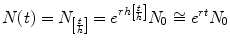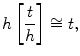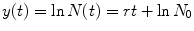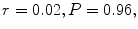Iannelli Mimmo - An Introduction to Mathematical Population Dynamics: Along the Trail of Volterra and Lotka

An Introduction to Mathematical Population Dynamics: Along the Trail of Volterra and Lotka — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "An Introduction to Mathematical Population Dynamics: Along the Trail of Volterra and Lotka" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

1234567...111

Part I
The growth of a single population

Springer International Publishing Switzerland 2014

Mimmo Iannelli and Andrea Pugliese An Introduction to Mathematical Population Dynamics UNITEXT 10.1007/978-3-319-03026-5_1

1. Malthus, Verhulst and all that

Mimmo Iannelli 1 and Andrea Pugliese 1

(1)

Department of Mathematics, University of Trento, Italy

Apparently, no book has been so extensively discussed by people who seem not to have read it, as it happens with the Essay on the Principle of Population by Mr. Malthus.

Such a harsh note by the editor, against the comments received by the Essay , takes us back to the atmosphere of those times and to the discussions that the Principle of population sustained by Thomas Robert Malthus, caused and fed since the first edition of the book in 1798. Actually this Principle can be stated in a few words:

population, when unchecked, increases in a geometrical ratio; subsistence increases only in an arithmetical ratio.

Projected to the future, such a mechanism produces catastrophic scenarios that, rightly or wrongly, when the Essay was published, were the object of great discussions and quarrels (see and the introduction to that volume, in Italian, for an interesting presentation). In fact, the thesis presented by Malthus in his famous book is part of a wide discussion between the conservative views (supported by Malthus) and the optimistic ones of the Enlightenment philosophers (especially Godwin and Condorcet) who supported a Theory of Progress . Right or wrong in his conclusions, Malthus however deserves the merit of having pointed out, about two hundred years ago, the problems related to demographic expansion.

Since the publication of the Essay , the name of Malthus is associated to exponential growth and in fact the model we will present at the beginning of this chapter is named after him. Actually, in the context of the Essay , as in other demographic studies, the use of an exponential curve to fit experimental data is essentially empirical, while the modeling viewpoint that we introduce in aims at obtaining exponential growth as the consequence of a priori constitutive assumptions. This approach will be maintained throughout the chapter where different mechanisms regulating intraspecific competition and exogenous effect will be introduced and discussed.

1.1 1.1 A look at exemplary data

The empirical approach to data description can be conveniently illustrated by exemplary data from the demographic context. In fact in we present classical numbers of a human population, provided by census institutions. Actually, demographic data have received much attention for thousands of years since, as it is obvious, man has initially paid much attention to most important events like births, deaths, diseases Thus we can take advantage of rather accurate observations.

Table 1.1

U.S.A. population

year	individuals a	rate
1790	3,929
1800	5,308	0,035
1810	7,240	0,036
1820	9,638	0,033
1830	12,861	0,033
1840	17,064	0,033
1850	23,192	0,036
1860	31,443	0,036
1870	38,558	0,023
1880	50,189	0,030
1890	62,980	0,025
1900	76,212	0,021
1910	92,228	0,021
1920	106,021	0,015
1930	123,203	0,016
1940	132,165	0,007
1950	151,326	0,015
1960	179,323	0,019
1970	203,302	0,013
1980	226,456	0,011
1990	255,712	0,010
2000	285,003	0,013

a millions

In data are reported by 10-years steps and the third column shows the growth rate of the population, i.e. the yearly relative change of the population. Namely, if N i denotes the number of individuals in the year i and h the length of the time interval (in the table h = 10 years ), then the growth rate can be defined through the formula

When the growth rate is approximately constant (as in the first part of , but also for the years 19001930) data can be represented through an exponential curve. In fact, we have the equation

(1.1)

and, iterating from i = 0 we get

and we see that the population undergoes geometrical increase or decrease if > 0 or < 0 respectively.

If now we suppose that holds for h small enough, the previous formula can be written using the exponential function as

and, adopting a time-continuous framework, for a given fixed time t the number of individuals N ( t ) is approximately given by

(1.2)

where we have approximated

and the approximation is better as h is smaller.

A procedure to fit data with an exponential curve, estimating the best value of the parameter r , is to apply the least square method , fitting a line to the data of is transformed into the line

with slope r and intercept y o = ln N 0. Then, the least square procedure applied to the data of provides the following values

Next page

1234567...111

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

Similar books «An Introduction to Mathematical Population Dynamics: Along the Trail of Volterra and Lotka»

Look at similar books to An Introduction to Mathematical Population Dynamics: Along the Trail of Volterra and Lotka. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.

Sydney H. Coontz

Population Theories and their Economic Interpretation

Thomas Robert Malthus

An Inquiry Into the Nature and Progress of Rent and the Principles by Which It Is Regulated

Paul Neurath

From Malthus to the Club of Rome and Back: Problems of Limits to Growth, Population Control and Migrations

Thomas Malthus

An Essay on the Principle of Population and Other Writings

Michael Schaub

Integrated Population Models Theory and Ecological Applications with R and JAGS

Malthus Thomas Robert

Malthus: A Very Short Introduction

Berry John

Mathematical Modelling

Thomas Robert Malthus

An Essay on the Principle of Population: The 1803 Edition

Diekmann O.

Mathematical tools for understanding infectious diseases

Michael A. Woodley

Historical Variability in Heritable General Intelligence: Its Evolutionary Origins and Socio-Cultural Consequences

Derek Holton

A First Step to Mathematical Olympiad Problems

Malthus Thomas-Robert

An Essay on the Principle of Population

Discussion, reviews of the book An Introduction to Mathematical Population Dynamics: Along the Trail of Volterra and Lotka and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.