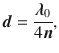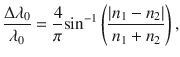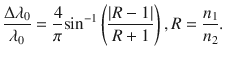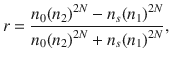LitArk » Books » Home and family

Ikhmayies - Advances in Silicon Solar Cells

Here you can read online Ikhmayies - Advances in Silicon Solar Cells full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. City: Cham, year: 2018, publisher: Springer International Publishing, genre: Home and family. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:

Romance novel Science fiction Adventure Detective Science History Home and family Prose Art Politics Computer Non-fiction Religion Business Children Humor

Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.

Book:
Advances in Silicon Solar Cells
Author:
Ikhmayies / Shadia
Publisher:
Springer International Publishing
Genre:
Books / Home and family
Year:
2018
City:
Cham
Rating:
5 / 5
Favourites:
Add to favourites
Your mark:
- 100
- 1
- 2
- 3
- 4
- 5

Description
Author's other books
Similar books

Advances in Silicon Solar Cells: summary, description and annotation

We offer to read an annotation, description, summary or preface (depends on what the author of the book "Advances in Silicon Solar Cells" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.

This book provides a review of all types of silicon solar cells. The scope includes monocrocrystalline Si solar cells, polycrystalline and amorphous thin-film silicon solar cells, and tandem solar cells. Production, treatment and development of these devices are reviewed. Limitations of these devices, design optimization, testing and fabrication methods are covered. In addition, current status and future prospects for the further development of silicon solar cells are addressed. Special emphasis is given to methods of attaining high efficiency and thereby cost-effective solar power. The aim of the book is to provide the reader with a complete overview about the recent advances in the structure and technology of all generations of silicon solar cells.

Ikhmayies: author's other books

Who wrote Advances in Silicon Solar Cells? Find out the surname, the name of the author of the book and a list of all author's works by series.

Advances in Silicon Solar Cells — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Advances in Silicon Solar Cells" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓

↑

Reset

Interval:

↓

↑

Bookmark:

Make

Springer International Publishing AG 2018

Shadia Ikhmayies (ed.) Advances in Silicon Solar Cells

Effective Light Management in Thin Silicon Wafers

Zhi-Peng Ling 1

(1)

Department of Electrical & Computer Engineering, National University of Singapore, Solar Energy Research Institute of Singapore, Singapore, Singapore

Zhi-Peng Ling

Email:

Abstract

Crystalline silicon (c-Si)-based photovoltaics have dominated the global market share over the past decade. To progress toward utility-scale adoption, cost reduction plans are necessary, in which one option is to reduce the silicon material used. This comes at a cost of lower photo-absorption and generation, particularly for near-infrared photons due to their much higher absorption depth as compared to short-wavelength photons. In this chapter, the different methods to enhance light trapping for near-infrared photons are mentioned, and in particular the methodology on the proper design of a one-dimensional conductive distributed Bragg reflector (DBR) scheme is introduced. Both experimental and simulation results in this chapter consistently demonstrate the feasibility of integrating a conductive DBR scheme at the rear of a heterojunction silicon wafer solar cell (a type of c-Si-based photovoltaics technology) for enhanced photo-generation at the target long-wavelength regions (i.e., 900 200 nm). The methodology presented here can be easily extended to other target wavelengths of interest and also not limited to solar cells applications alone.

Keywords

Distributed Bragg reflectors Light trapping Silicon solar cells

Introduction

Crystalline silicon- based photovoltaics [ shows that L 160 m at = 1000 nm and L 0.1 m at = 400 nm. Hence, it is clear that thinner silicon wafers are not able to absorb long-wavelength photons effectively, which leads to reduced photo-generation and a lower short-circuit current density ( J SC). Consequently, the key challenge with thinner wafers is to enhance the optical path length by trapping long-wavelength photons within the absorber for a duration as long as possible in order to increase the photo-generation rate.

Fig. 1

Wavelength-dependent absorption coefficient and corresponding absorption depth for a silicon wafer

Different Methods for Light Trapping

Light-trapping schemes can be implemented at both the front and rear surfaces of the solar cell . Several approaches had been adopted, which include randomly roughened surfaces [] to enhance the photo-generation due to a higher degree of scattering and reflection. However, a careful optimization of the periodicity and the height of the gratings is required, which increases process complexity and costs.

On the other hand, utilizing a simple one-dimensional distributed Bragg reflector for rear-surface light trapping appears to be an attractive option as well. Previous studies had included using at least one insulating or moderately conducting layer such as combinations of Si/Si3N4 or Si/SiO2 stacks []. Considering the ease and merits of integrating a DBR scheme at the rear of a thin silicon wafer for light trapping, the subsequent sections focus on the proper design of a DBR-based light-trapping scheme.

Design Methodology of a Distributed Bragg Reflector

Similar to a semiconductor with a defined bandgap within which no electronic states can exist, an analogous situation is observed for photons in a distributed Bragg reflector (equivalently a one-dimensional photonic crystal [. If films with a periodically varying dielectric function (or index of refraction) are stacked together, the reflections and refractions of light from the various interfaces can create photonic bandgaps , which will forbid photon propagation in certain directions for a certain (designed) photon wavelength 0 within a certain bandwidth 0.

Fig. 2

Schematic of a one-dimensional photonic crystal (distributed Bragg reflector, DBR). The DBR consists of several DBR unit blocks. Each DBR unit block consists of alternating layers of two materials with different dielectric constants, with a period a (From Ref. [])

To realize the DBR, periodic stacks of two layers (DBR unit blocks) with different refractive indices n 1 and n 2 are chosen, whereby n 1 > n 2. For the DBR unit block, the thickness of the individual layers d 1 and d 2 is typically chosen to satisfy a quarter-wavelength stack at the target peak reflectance wavelength 0 [] as:

Advances in Silicon Solar Cells - image 3

(1)

where d is a function of the target peak reflectance wavelength 0 and the refractive index n of that layer at that wavelength. The objective of using a quarter-wavelength stack is to achieve quarter-wavelength optical thickness for the individual layers, so that for a DBR with multiple stacks of periodic DBR unit blocks, only wavelengths within the designed peak reflectivity regions interfere constructively, while the rest interfere destructively to give lower or zero reflectance. The overall optical reflectance at the target wavelength and its bandwidth is thus highly enhanced, so that the designed distributed Bragg reflector acts as a mirror.

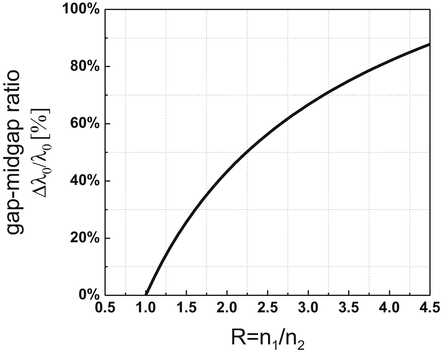
It is also of relevance to find out the wavelength range (bandwidth) around the target peak reflectance wavelength for which high optical reflectance is expected. From experimental and theoretical analysis, the bandwidth can be approximated via the gapmidgap ratio 0/0 []:

2 where 0 denotes the bandwidth at the target peak reflectance wavelength 0 - photo 4

(2)

where 0 denotes the bandwidth at the target peak reflectance wavelength 0. The bandwidth 0 defines the photonic gap between the first two bands of a quarter-wavelength stack, analogous to a bandgap in a semiconductor material. If we define a refractive index contrast R such that R = n 1/ n 2, the above equation can be rewritten as:

$3 With an increasing refractive index contrast the gapmidgap ratio 00 - photo 5$

(3)

With an increasing refractive index contrast, the gapmidgap ratio 0/0 increases as evident in Fig. , indicating a wider reflection bandwidth 0 for the DBR unit block.

$Fig 3 Gapmidgap ratio 00 of a DBR unit block as a function of the refractive - photo 6$

Fig. 3

Gapmidgap ratio 0/0 of a DBR unit block as a function of the refractive index contrast R = n 1/ n 2

The optical reflectance of a DBR can be expressed as []:

$4 where n 0 n 1 n 2 and n s are the refractive indices of the ambient - photo 7$

(4)

where n 0 , n 1 , n 2, and n s are the refractive indices of the ambient, of Bragg material 1, of Bragg material 2, and of the substrate, respectively, and N is the number of DBR unit blocks making up the DBR. From Fig. shows that a hypothetical DBR with a refractive index contrast of 1.5 would require 8 DBR unit blocks to approach unity reflection, whereas a DBR with a refractive index contrast of 3.5 would only need three DBR unit blocks. Thus, when considering DBRs, it is logical to utilize materials with a high refractive index contrast in order to reduce the number of DBR unit blocks required, as well as to benefit from a wider reflection bandwidth.

Light

Font size:

↓

↑

Reset

Interval:

↓

↑

Bookmark:

Make

Similar books «Advances in Silicon Solar Cells»

Look at similar books to Advances in Silicon Solar Cells. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.

Amanda Little

Power Trip: From Oil Wells to Solar Cells---Our Ride to the Renewable Future

Lee Elliott

Sun Solar Cooking: Fail-Proof, Guaranteed Solar Cooking Strategies

Theodore Ong

Solar Power: Economic Disaster

Inamuddin (editor)

Fundamentals of Solar Cell Design

Masahiro Hiramoto

Organic Solar Cells: Energetic and Nanostructural Design

Smith

ILL DIY Solar Projects

Kuang Ken.

Conveyor Belt Furnace Thermal Processing

Findley

Solar Power for Your Home

Baiano Reeves

Solar Power DIY Handbook: So, You Want To Connect Your Off-Grid Solar Panel to a 12 Volts Battery?

$Christian Stefano Schuster - Diffractive Optics for Thin-Film Silicon Solar Cells$

$Diffractive Optics for Thin-Film Silicon Solar Cells$

Christian Stefano Schuster

Diffractive Optics for Thin-Film Silicon Solar Cells

Takeo Oku

Solar Cells and Energy Materials

Kentaro Ito

Copper Zinc Tin Sulfide-Based Thin Film Solar Cells

Reviews about «Advances in Silicon Solar Cells»

Discussion, reviews of the book Advances in Silicon Solar Cells and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.