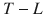Miguel Mujica Mota - Applied Simulation and Optimization 2
Here you can read online Miguel Mujica Mota - Applied Simulation and Optimization 2 full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. City: Cham, publisher: Springer International Publishing, genre: Home and family. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Applied Simulation and Optimization 2
- Author:
- Publisher:Springer International Publishing
- Genre:
- City:Cham
- Rating:3 / 5
- Favourites:Add to favourites
- Your mark:
Applied Simulation and Optimization 2: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Applied Simulation and Optimization 2" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
International airports are complex systems that require efficient operation and coordination of all their departments. Therefore, suitable personnel and equipment scheduling solutions are vital for efficient operation of an airport as a system. Many general solutions for fleet scheduling are available; however, there is a lack of scheduling solutions for airport ground crews, especially for work groups with overlapping skills. In the presented case, a scheduling solution for airport ground crew and equipment in a small international airport is described. As analytical methods are unsuitable for the system in question, the proposed scheduling solution is based on heuristics. A combined agent based and discrete event simulation model was developed to validate and improve the heuristic algorithms until they produced acceptable schedules and shifts. The algorithms first compute the requirements for workforce and equipment based on flight schedules and stored heuristic criteria. Workforce requirements are then optimized using time shifting of tasks and task reassignments, which smooth the peaks in workforce requirements, and finally the simulation model is used to verify the generated schedule. The scheduling procedure is considerably faster than manual scheduling and allows dynamic rescheduling in case of disruptions. The presented schedule generation and optimization solution is flexible and adaptable to other similar sized airports.
Miguel Mujica Mota: author's other books
Who wrote Applied Simulation and Optimization 2? Find out the surname, the name of the author of the book and a list of all author's works by series.
Miguel Mujica Mota
Hanne Bruun
Sheikh Imran Ishrat
Gündüz Ulusoy
Norman Ashford
Richard de Neufville
Applied Simulation and Optimization 2 — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Applied Simulation and Optimization 2" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Light
Font size:
↓
↑
Reset
Interval:
↓
↑
Bookmark:
Make
Part I
Novel Tools and Techniques in Simulation Optimization
Novel Tools and Techniques in Simulation Optimization
Springer International Publishing AG 2017
Miguel Mujica Mota and Idalia Flores De La Mota (eds.) Applied Simulation and Optimization 2 10.1007/978-3-319-55810-3_1A Conceptual Framework for Assessing Congestion and Its Impacts
Jennie Lioris 1
(1)
cole des Ponts-ParisTech, Champs-sur-Marne, France
(2)
California PATH, Richmond, USA
(3)
University of California, Berkeley, Berkeley, USA
Jennie Lioris
Email:
Alexander Kurzhanskiy
Email:
Pravin Varaiya (Corresponding author)
Email:
Abstract
In urban areas, intersections are the main constraints on road capacity while traffic flows do not necessarily directly conform to the speed-flow relationship. It is rather the signal timing and the interplay between the clearing rate of each intersection which determines the formation and duration of congestion. Junctions often differ in their design and throughput. General conclusions on the relationship between vehicle speed and traffic flows on a junction link are rarely possible. Well-adapted models are required for a comprehensive study of the behaviour of each intersection as well for the interactions between junctions. This chapter assesses the potential benefits of adaptive traffic plans for improved network management strategies, under varying traffic conditions. Queueing analysis in association with advanced simulation techniques reveal congestion mitigation actions when the pre-timed actuation plan is replaced by the max-pressure feedback control. The case of unpredicted local demand fluctuation is studied, where uncontrolled congestion is progressively propagated to the entire network under the open-loop policy. Travel-time variability is measured under both plans and within all traffic schemes while frequency of stop-and-go actions are also encountered. Reliability of predictable trip durations is a major factor to be considered when ensuring on time arrivals and the related costs when the time is converted into benefits.
Keywords
Traffic responsive signal Adaptive control Pre-timed control Max-pressure practical policy Discrete event simulation Performance evaluation Queueing network modelIntroduction
In contrast to freeways, urban traffic is distinguished by the existence of junctions and/or roundabouts involving conflicting traffic streams and thus interrupting vehicle flows. Intersections play a major role in determining the quality and volume of traffic in arterial networks by arbitrating conflicting movements in order to allow users to share the same road space sequentially.
Traffic control and signal coordination contribute to improve travel conditions by reducing frequent vehicle stops and queue lengths. More precisely, signal coordination may contribute to an optimised use of the current infrastructure, by establishing platoon type vehicle departures.
Automobile dependent cities often associated with large traffic volumes, tend to imply poor road performance especially when varying travel schemes occur forcing the related transportation structure towards heavy traffic or even congestion states. Moreover, spatial complexity is characterised by even more complex journeys difficult to be predicted and consequently controlled. Activity changes influence spatial distribution and consequently complex travel patterns are manifested and congestion is possible.
Classical congestion management policies maximise the ability of urban areas to deal with current and expected demand. Such flow-based management policies, associate capacities to road links expressed in flow and density. Under that scope, network performance is increased when higher density and flows are reached.
Alternatively, cost-congestion approaches involve an economically optimal traffic level for each road and tend to measure the congestion cost incurring when traffic exceeds the optimum levels by taking into consideration the related road demand and supply.
Many traditional traffic managements aiming to increase road capacity and thus to mitigate congestion impacts by improving traffic operations while others seek to involve road infrastructure and/or to shift roadway demand to public transportation. Although such approaches are suited for particular congestion types such as bottlenecks they can deliver long-lasting results when they are paired with other policies controlling the newly created capacity. Non-recurrent congestion caused by unplanned events influencing the system behaviour which frequently becomes unpredictable, and may cause extreme congestion conditions and/or become system-wide. A vehicle breakdown may create bottlenecks, prohibiting transit in a part of road or obliging other vehicles to deviate and thus varying demand patterns may be caused. Similar effects can occur from other events such as crashes, bad weather, work zones etc.
Congestion influences both travel times (indicators concerning mostly policy makers) and the reliability of the predicted travel conditions (indicators interesting to road users). There is no single congestion metric which is appropriate for all purposes. Consequently, quantitative and qualitative metrics should be provided when measuring congestion such as queue lengths and related duration, variance of travel times etc.
This work explores the effectiveness of the currently available road infrastructure management under open and close loop signal plans within various traffic contexts. The outline of this paper is as follows:
Section reveals the simulation advantages, where a detailed analysis allows a complete reconstruction of the simulated scenario. Consequently, any system observation can be deeply examined and consequently justified. An illustrative example is discussed.
Traffic Control: Problem Statement and Timing Plans
This section presents the dealing problem in order to understand the insights resulting from the framework on traffic management as discussed in the next sections. Moreover, an open loop control scheme and versions of Max-Pressure feedback algorithm are briefly introduced. A much more extensive study as well all theoretical properties of Max-Pressure control are presented in [] where stability guarantees are also provided.
2.1 Problem Formulation
Let us consider an intersection n . A phase ( i , j ) indicates a permitted movement from an incoming link i of node n towards an outgoing link j . A stage 
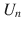
indicates a set of simultaneously compatible phases of node n and is represented by a binary matrix such that: 
The set of all considered intersection stages is denoted by 
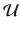
. For simplicity, the optimisation horizon is divided into intervals or cycles of fixed width, each one comprised of T time periods. Let 
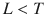
denote the idle time, that is the time period during which no phase is actuated and occurring within two different stage switches. This time corresponds to amber lights, pedestrian movements etc. Hence, the total available actuation period per cycle is 
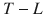
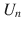indicates a set of simultaneously compatible phases of node n and is represented by a binary matrix such that: 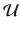. For simplicity, the optimisation horizon is divided into intervals or cycles of fixed width, each one comprised of T time periods. Let 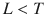denote the idle time, that is the time period during which no phase is actuated and occurring within two different stage switches. This time corresponds to amber lights, pedestrian movements etc. Hence, the total available actuation period per cycle is Light
Font size:
↓
↑
Reset
Interval:
↓
↑
Bookmark:
Make
Similar books «Applied Simulation and Optimization 2»
Look at similar books to Applied Simulation and Optimization 2. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
Hanne Bruun
Sheikh Imran Ishrat
Gündüz Ulusoy
Norman Ashford
Richard de Neufville
Reviews about «Applied Simulation and Optimization 2»
Discussion, reviews of the book Applied Simulation and Optimization 2 and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.