Peter Farrell - Math Adventures with Python

AN ILLUSTRATED GUIDE TO EXPLORING MATH WITH CODE

BY PETER FARRELL

San Francisco

MATH ADVENTURES WITH PYTHON. Copyright 2019 by Peter Farrell.

All rights reserved. No part of this work may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopying, recording, or by any information storage or retrieval system, without the prior written permission of the copyright owner and the publisher.

ISBN-10: 1-59327-867-5

ISBN-13: 978-1-59327-867-0

Publisher: William Pollock

Production Editor: Meg Sneeringer

Cover Illustration: Josh Ellingson

Developmental Editor: Annie Choi

Technical Reviewer: Patrick Gaunt

Copyeditor: Barton D. Reed

Compositors: David Van Ness and Meg Sneeringer

Proofreader: James Fraleigh

The following images are reproduced with permission:

; CC-BY-SA-3.0);

.

For information on distribution, translations, or bulk sales, please contact No Starch Press, Inc. directly:

No Starch Press, Inc.

245 8th Street, San Francisco, CA 94103

phone: 1.415.863.9900;

www.nostarch.com

A catalog record of this book is available from the Library of Congress.

No Starch Press and the No Starch Press logo are registered trademarks of No Starch Press, Inc. Other product and company names mentioned herein may be the trademarks of their respective owners. Rather than use a trademark symbol with every occurrence of a trademarked name, we are using the names only in an editorial fashion and to the benefit of the trademark owner, with no intention of infringement of the trademark.

The information in this book is distributed on an As Is basis, without warranty. While every precaution has been taken in the preparation of this work, neither the authors nor No Starch Press, Inc. shall have any liability to any person or entity with respect to any loss or damage caused or alleged to be caused directly or indirectly by the information contained in it.

This book is dedicated to all my students, from whom Ive learned so much.

Peter Farrell was a math teacher for eight years, starting first as a Peace Corps volunteer in Kenya. He then worked as a computer science teacher for three years. After reading Seymour Paperts Mindstorms and being introduced to Python by a student, he was inspired to bring programming into math class. He is passionate about using computers to make learning math more relevant, fun, and challenging.

Paddy Gaunt graduated in engineering within weeks of the birth of the IBM PC and its associated MS DOS. Much of the rest of his career has revolved around implementing mathematical or technical concepts in practical software. Recently, he reformed links with Cambridge University (UK) when he became lead developer of pi3d, a python module for 3D graphics initially designed to run on the Raspberry Pi computer.

1
DRAWING POLYGONS WITH THE TURTLE MODULE

2
MAKING TEDIOUS ARITHMETIC FUN WITH LISTS AND LOOPS

3
GUESSING AND CHECKING WITH CONDITIONALS

4
TRANSFORMING AND STORING NUMBERS WITH ALGEBRA

5
TRANSFORMING SHAPES WITH GEOMETRY

6
CREATING OSCILLATIONS WITH TRIGONOMETRY

7
COMPLEX NUMBERS

8
USING MATRICES FOR COMPUTER GRAPHICS AND SYSTEMS OF EQUATIONS

9
BUILDING OBJECTS WITH CLASSES

10
CREATING FRACTALS USING RECURSION

11
CELLULAR AUTOMATA

12
SOLVING PROBLEMS USING GENETIC ALGORITHMS

Id like to thank Don The Mathman Cohen for showing me how fun and challenging learning real math can be; Seymour Papert for proving that coding belongs in math class; Mark Miller for giving me a chance to put my ideas into action; Hansel Lynn and Wayne Teng of theCoderSchool, who let me continue to have fun coding with students; and Ken Hawthorn for sharing my projects at his school. Thank you to my No Starch editors, Annie Choi, Liz Chadwick, and Meg Sneeringer, for all your help making this a much better book, and to Paddy Gaunt, whose input is visible all over this book. This book wouldnt exist without you all. Thank you to everybody who said noyou gave me the energy to keep going. Finally, thank you to Lucy for always believing in me.

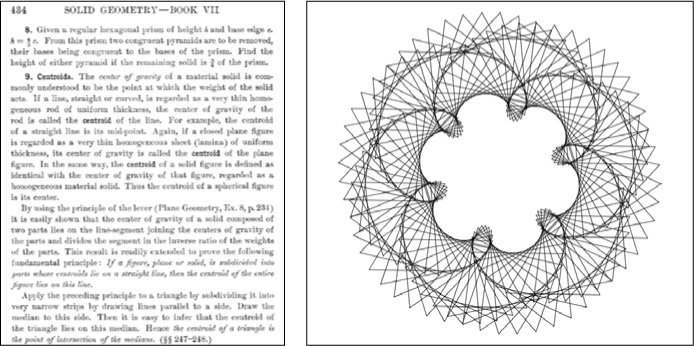
Which approach shown in would you prefer? On the left, you see an example of a traditional approach to teaching math, involving definitions, propositions, and proofs. This method requires a lot of reading and odd symbols. Youd never guess this had anything to do with geometric figures. In fact, this text explains how to find the centroid, or the center, of a triangle. But traditional approaches like this dont tell us why we should be interested in finding the center of a triangle in the first place.

Figure 1: Two approaches to teaching about the centroid

Next to this text, you see a picture of a dynamic sketch with a hundred or so rotating triangles. Its a challenging programming project, and if you want it to rotate the right way (and look cool), you have to find the centroid of the triangle. In many situations, making cool graphics is nearly impossible without knowing the math behind geometry, for example. As youll see in this book, knowing a little of the math behind triangles, like the centroid, will make it easy to create our artworks. A student who knows math and can create cool designs is more likely to delve into a little geometry and put up with a few square roots or a trig function or two. A student who doesnt see any outcome, and is only doing homework from a textbook, probably doesnt have much motivation to learn geometry.

In my eight years of experience as a math teacher and three years of experience as a computer science teacher, Ive met many more math learners who prefer the visual approach to the academic one. In the process of creating something interesting, you come to understand that math is not just following steps to solve an equation. You see that exploring math with programming allows for many ways to solve interesting problems, with many unforeseen mistakes and opportunities for improvements along the way.

This is the difference between school math and real math.

What do I mean by school math exactly? In the US in the 1860s, school math was preparation for a job as a clerk, adding columns of numbers by hand. Today, jobs are different, and the preparation for these jobs needs to change, too.

People learn best by doing. This hasnt been a daily practice in schools, though, which tend to favor passive learning. Doing in English and history classes might mean students write papers or give presentations, and science students perform experiments, but what do math students do? It used to be that all you could actively do in math class was solve equations, factor polynomials, and graph functions. But now that computers can do most of those calculations for us, these practices are no longer sufficient.