Christophe Bourlier - Shadowing Function from Randomly Rough Surfaces: Derivation and applications
Here you can read online Christophe Bourlier - Shadowing Function from Randomly Rough Surfaces: Derivation and applications full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2019, publisher: Scitech Publishing, genre: Home and family. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Shadowing Function from Randomly Rough Surfaces: Derivation and applications
- Author:
- Publisher:Scitech Publishing
- Genre:
- Year:2019
- Rating:5 / 5
- Favourites:Add to favourites
- Your mark:
Shadowing Function from Randomly Rough Surfaces: Derivation and applications: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Shadowing Function from Randomly Rough Surfaces: Derivation and applications" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
The shadowing function is an important element in the simulation and calculation of how electromagnetic waves scatter at randomly rough surfaces. Its derivation and use is an active, interdisciplinary area of research with practical applications in fields such as radar, optics, acoustics, geoscience, computer graphics and remote sensing.
This book addresses the general problem of the derivation of the shadowing function from randomly rough surfaces. The authors present an overview of theory and advances of this topic by detailing recent progress. Firstly, the simpler problems are investigated (monostatic case - 1D surface - one reflection) progressing in difficulty to more complicated problems (bistatic case - 2D surface - multiple reflections). In addition, the authors focus on the introduction of the simplifying assumptions to derive closed-form expressions of the shadowing function and quantify their impact on the accuracy of the resulting models. Applications of the shadowing function in problems encountered in physics are also addressed.
The problem of the derivation of the shadowing function from a rough surface is at the boundary between several scientific communities, each with its terminology. This book makes the link between these different communities and will help the reader to understand the theoretical aspects of this problem while giving practical applications.
Christophe Bourlier: author's other books
Who wrote Shadowing Function from Randomly Rough Surfaces: Derivation and applications? Find out the surname, the name of the author of the book and a list of all author's works by series.
Shadowing Function from Randomly Rough Surfaces: Derivation and applications — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Shadowing Function from Randomly Rough Surfaces: Derivation and applications" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Font size:
Interval:
Bookmark:
I am grateful to Professor Joseph Saillard (retired) and Grard Berginc who have initialized this work during my PhD Thesis. I would also like to thank the National Center for Scientific Research by whom I am employed and ONERA with whom I worked to include the resolution of the infrared camera.
Shadowing function from one-dimensional surface
Christophe Bourlier
1IETR Laboratory, CNRS, Nantes, France
In this chapter, shadowing function from a randomly rough one-dimensional surface is derived by ignoring multiple reflections (Chapter 3).
First, a brief history and review of the derivation of the shadowing function is addressed.
Next, the special case of a monostatic configuration, for which the positions of the transmitter and receiver are the same, is investigated. This allows us to detail the rigorous derivation of the shadowing function and to discuss on the introduction of the simplifying assumptions need to obtain a closed-form expression of the statistical shadowing function. It depends then on the slope 
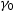and on the height 
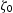of any arbitrary point on the surface, which are random variables.
Section 1.3 gives closed-form expressions of the statistical averages obtained by calculating the expected values of the statistical shadowing function over 
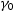or/and 
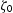. This requires the knowledge of the joint PDF (probability density function) of 
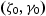assumed to be uncorrelated.
In order to quantify the effect of the correlation between 
and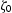 
, Section 1.4 deals with the case of a correlated process assumed to be Gaussian. This Gaussian assumption leads to closed-form expressions of the average shadowing functions.
Section 1.5 validates the different formulations by comparing them with a benchmark ray-tracing method, and a Monte Carlo (MC) process is applied to access the mean values.
The last two sections generalize the formulations to the bistatic cases in reflection (receiver above the surface) and transmission (receiver below the surface), for which the transmitter and receiver positions are distinct in the space.
The problem of wave scattering the from a rough surface in the presence of shadowing was first considered analytically by Bass and Fuks [] formulations, who retained the first term of the series. Moreover, Smith used the Wagner approach by introducing a normalization function.
For monostatic and bistatic configurations, these authors assumed a one-dimensional surface with an uncorrelated Gaussian process of surface heights and slopes. This means that the statistical illumination function is independent of the surface height autocorrelation function. More recently, for one- and two-dimensional surfaces with Gaussian statistics, Bourlier et al. [].
As shown in . The rays coming from the surface and propagating with respect to the direction 
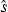are blocked by the surface itself. This phenomenon is called the shadowing effect.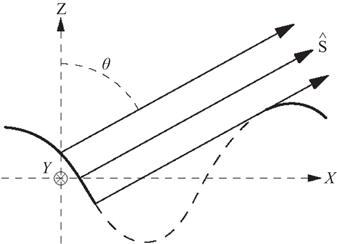
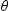Figure 1.1 Shadowing effect of rough surfaces. The observation direction forms an angle 
with the zenith. The 
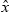direction corresponds to the horizontal direction of the receiver. The dashed part of the surface lies in the shadow of the receiver, whereas the solid part of the surface is seen by the receiver
The shadowing effect depends on the observation direction 
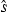and the shape of the surface related to the roughness (heights, slopes, etc.). For instance, a flat surface is always fully illuminated in all observation directions 
.
From a pure geometrical point of view, the following features can be drawn:
- In the case where
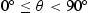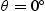, which means that the emission ray is propagating vertically upward, no emission ray is blocked (see (a)). - In the case where
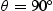, which means that the emission ray is propagating horizontally towards the receiver located at the level of the horizon, nearly all emission rays are blocked, except for the few ones at the edge of the surface (see (b)). - The higher the point is, the more likely it is illuminated. The highest point of the surface is illuminated, as no other point can shadow it (see (c), point
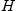). Indeed, if a surface point is in the shadow of the receiver, its emission ray along 
reaches the surface at some other point. - The surface points with slopes
in the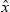 
direction (corresponds to the horizontal direction of the receiver) being larger than the slope 
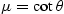of the emission ray lie in the shadow of the receiver, as the local angle of incidence(d)) 
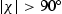, which is not physical.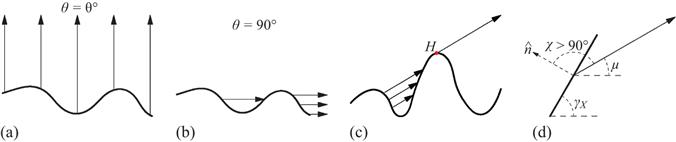
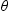Figure 1.2 Four physical features of the shadowing effect. (a) Case 
. (b) Case = 90. (c) Shadowing versus the height of the surface point. (d) Shadowing versus the slope of the surface point
As predicted by items 1 and 2 in the above list, shadowing becomes more and more significant as the zenith observation angle increases. For large 
, shadowing is too significant to be neglected.
For instance, in measurements of sea surface radiation, the receiver located near the sea surface (e.g., on a ship or an airplane) satisfies this condition. In addition, if the wind speed above the sea surface is high, the surface slope standard deviation is also high (related to item 4 of the above list), which increases the shadowing effect.
Font size:
Interval:
Bookmark:
Similar books «Shadowing Function from Randomly Rough Surfaces: Derivation and applications»
Look at similar books to Shadowing Function from Randomly Rough Surfaces: Derivation and applications. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
Discussion, reviews of the book Shadowing Function from Randomly Rough Surfaces: Derivation and applications and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.