Contents
List of Figures
List of Tables
Guide
Pagebreaks of the print version

Mathematics for Economics
fourth edition
Michael HoyJohn LivernoisChris McKennaRay ReesThanasis Stengos
The MIT Press
Cambridge, Massachusetts
London, England
2022 Massachusetts Institute of Technology
All rights reserved. No part of this book may be reproduced in any form by any electronic or mechanical means (including photocopying, recording, or information storage and retrieval) without permission in writing from the publisher.
The MIT Press would like to thank the anonymous peer reviewers who provided comments on drafts of this book. The generous work of academic experts is essential for establishing the authority and quality of our publications. We acknowledge with gratitude the contributions of these otherwise uncredited readers.
Library of Congress Cataloging-in-Publication Data
Names: Hoy, Michael, 1953 September 22- author. | Livernois, John Richard, author. | McKenna, C. J., author.
Title: Mathematics for economics / Michael Hoy, John Livernois, Chris McKenna, Ray Rees, Thanasis Stengos.
Description: Fourth Edition. | Cambridge, Massachusetts: The MIT Press, 2022. | Revised edition of the authors Mathematics for economics, c2011.
Identifiers: LCCN 2021017758 | ISBN 9780262046626 (hardcover)
Subjects: LCSH: Economics, Mathematical.
Classification: LCC HB135.H69 2022 | DDC 511/.8dc23
LC record available at https://lccn.loc.gov/2021017758
d_r0
This book is dedicated to our families:
Maureen, Alexis, and Joshua
Ali and Becky
Jane, James, and Kate
Denny, Zac, and Dan
Bieke, Yanna, Mariana, and Dominiek
Contents
List of Figures
Venn diagrams. (a) nonintersecting sets; (b) intersecting sets.
SV = S and SV = V when SV.
An example of a partition of U.
The set Z of integers.
The set Q of rational numbers.
 is irrational.
is irrational.
The set of real numbers, .
Points in 2.
Points in 3.
Boundary and interior points.
Euclidean distance in 2.
B(2).
B[(2, 3)].
B[(2, 3, 1)].
Convex combination in 2.
Convex combination in 3.
Convex and nonconvex sets in 2.
Graph of y = x2.
Composition of mappings.
Linear functions as in equation 2.16.
Linear function with a positive intercept.
A convex combination.
Quadratic functions.
Rectangular hyperbola.
Power functions axb: ++.
Exponential function aex: .
The logarithmic function log bx: + .
Strict concavity.
Strict convexity.
The function f(x) = x2 is strictly convex.
The function y = 2x1 + 3x2.
The function y = x12x22.
Level sets of the function y = 2x1 + 3x2.
Level sets of the function y = x12x22.
The first five terms of the sequence f(n) = 2n.
The first five terms of the sequence f(n) = 1/n.
The first five terms of the sequence f(n) = 1/n.
The first five terms of the sequence f(n) = (1)n.
The first five terms of the sequence f(n) = n2.
The first five terms of the sequence f(n) = (2)n.
Illustration that f(n) = (1)n has no limit (example 3.3).
Function y = 2x (with a demonstration that it is continuous at x = 3).
Function y = x32x2+1 (with a demonstration that it is continuous at x = 1/2).
This function is discontinuous at x = 0.
The function f(x) = 1/x2 is discontinuous at x = 0.
The function f(x) = 1/(x 1) is discontinuous at x = 1.
This function is discontinuous at x = 2.
The function y = (1/1, 050)x.
A salary schedule with a bonus payment.
A discontinuous income support function.
A continuous income-support function.
Marginal product of an input under a capacity constraint.
Revenue and profit functions of firm 1 for given prices of firm 2.
A tangent line.
A secant line.
Sequence of secants.
Slope of a secant depending on x.
Tangent line for y = x2 at the value x = 2.
A function with the same tangent line at two points.
Tangent line on a linear function.
dy = f(x) dx as an approximation to the change in y.
Accuracy of dy = f(x) dx as an approximation to y.
A case where the differential is an overestimate.
A case where the differential is an exact approximation.
A total cost function.
Relationship between the marginal and total cost functions for C(y) = y2.
A function with different left-hand and right-hand derivatives at point x = 1.
Piecewise linear income tax schedule.
Marginal income tax functiondiscontinuous.
A function with a domain that is a closed interval.
Constant function f(x) = c with zero slope.
Total revenue and marginal revenue of a competitive firm.
Linear demand with a constant slope.
Total product of labor with increasing marginal product.
Total product of labor with constant marginal product.
Total product of labor with decreasing marginal product.
Impact on a monopolists revenue of the sale of an additional q units.
Marginal revenue for a monopolist facing the inverse demand function p = 40 2q.
U-shaped marginal and average cost curves.
A case where more of an input is required to generate an extra unit of output as the initial level of output becomes higher.
Production function and associated cost function for example 5.20.
Function y = ex.
Elasticity changes along the demand function y = 50 2p.
The function f(x) = x2, x 0 and its first two derivatives.
The function f(x) = x2, x 0 and its first two derivatives.
The function f(x) = x2, xR, and its first two derivatives.
Possible shapes of strictly convex functions.
A strictly concave function: y = 10 x2.
The function 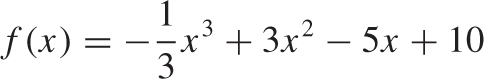 (example 5.31).
(example 5.31).
The function f(x) = (2/3)x3 + 10x2 + 5x.
.
The use of the total differential to approximate a change in the value of a function.
Example where the total differential overestimates the change in the functions value.
Example where the total differential underestimates the change in the functions value.
Depiction of indifference curves in mean-standard deviation space.
Illustration of the mean-value theorem.
(a) Neither a maximum nor a minimum exists; (b) no maximum exists; (c) no minimum exists.











 is irrational.
is irrational.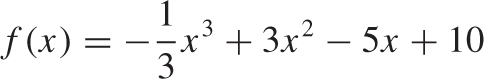 (example 5.31).
(example 5.31).