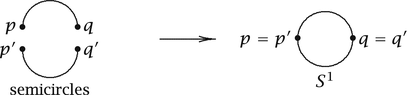1. 3-Sphere
Since the beginning of human civilization, man has struggled to understand his universe. Ironically, the Aristotle (384-322 BC ) spherical model, with earth at the center, was fundamental to Dantes (1265-1321 AD ) model which, in turn, underlies the so-called Einstein (1879-1955 AD ) Universe. In common language, the Aristotle model involves a solid ball with a spherical surface, and Dantes model adds a mirror-image solid ball to Aristotles and then joins them by gluing their surfaces. In 20th Century language, Dante constructed a three-sphere S 3; and the three sphere S 3 turned out to be fundamental to what is commonly called Einsteins Universe. All of these models involve spheres constructed inside universes of dimensions three and four.
But what does it mean to say spheres constructed inside universes of dimensions three and four ? And how can we think about and understand such spheres without getting bogged down in the mathematical jargon? In this chapter we answer these questions by using simple examples and pictures.
1 Spheres
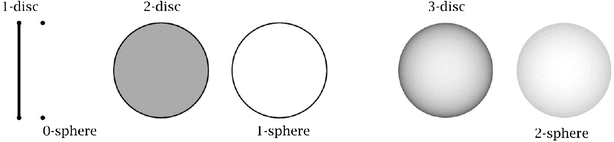
We focus on four types of spheres. Three of the four types are pictured in Figure below from left-to-right we see models of a 0-sphere (two points), a 1-sphere (circle), and a 2-sphere (surface of a ball which may be viewed as a seamless inflated balloon):
Fig. 1.1
A zero-sphere S 0, a one-sphere S 1, and a two-sphere S 2.
The fourth kind of sphere is the 3-sphere S 3. Unlike S 0, S 1, and S 2, we cannot picture S 3 because human vision is 3-dimensional it is impossible to picture S 3 within such a dimension-restricted visual universe.
But what does it mean to say 3- dimensional ? Historically, a precise definition of dimension did not appear until the early 1900s, and the definition involves some subtle mathematics. So we shall take another approach, namely, in the following few pages we shall use examples and pictures to convey the essence of 3-dimensional.
2 Why is it that we cannot see a 3-sphere?
To roughly appreciate why human vision does not allow us to picture S 3, consider the following S 2 analogy: On the left side of Figure we see the circle that Freddy sees, but Freddy sees the circle only from its edge.
Fig. 1.2
Freddy, with 2-dimensional vision, looks at a 2-sphere.
Freddy cannot see S 2 because S 2 contains points above and below his viewing plane. And to move off of the viewing plane, say in an up-down direction requires an extra dimension. Freddys vision, unlike human vision, does not include the extra up-down direction. So Freddy cannot see the 2-sphere S 2, while humans easily see S 2.
Intuitively at least, this example with Freddy motivates the belief that humans (with 3-dimensional vision) cannot see the 3-sphere S 3. Just as S 2 curves outside of any 2-dimensional plane, S 3 curves outside any 3-dimensional hyper plane.
Other facts illustrated in Figure extend to the 3-sphere S 3. Most notably, when Freddys visual plane intersects S 2 as indicated, he sees S 1. Step this experiment up one dimension, and we have the fact that when humans similarly look at S 3 , they see S 2.
In particular, when we look into the night sky and see a full moon, we may be seeing that part of a 3-sphere where it intersects our visual universe. (See Figure where Freddy has recovered his 3-dimensional vision.)
Fig. 1.3
Is it an S 3 intersecting my 3-dim visual plane?
3 Spheres and discs
Potatoes have skins, boiled eggs have shells, and planets have surfaces. But what does a potato, a boiled egg, and a planet illustrate ? Each provides an intuitive example of a solid ball bounded by a 2-sphere. To be sure, the bounding 2-spheres are represented by the skin, the shell, and the surface. We shall call a solid ball that contains its 2-sphere boundary a 3- disc .
Fig. 1.4
Discs with their spherical boundaries separately illustrated.
Let us step down to dimension two: Each flat side of a coin has a unique edge, an archery target has an area inside of a circle, and within a picture of a wheel we see an area bounded by a rim. At dimension two these are rough examples of a circular area bounded by a circle (one-sphere S 1). We shall refer to an area that contains its bounding circle ( S 1) as a 2- disc .
Now let us step down to dimension one: A needle has a sharp endpoint and a dull endpoint, a carpenter marks a line between two points, and a single human hair has a root and a tip. At dimension one these statements provide rough examples of a line segment bounded by two endpoints (zero-sphere S 0). We shall call a line segment that contains its bounding zero sphere S 0 a 1- disc .
4 Gluing discs
Lines and line segments are the simplest examples of one-dimensional objects a line and a 1-disc (line segment) [ p , q ] with endpoints p and q are pictured below where the dots indicate that the line extends indefinitely. A line does not stop, it has infinite length. In contrast, a line segment [ p , q ] is the connected part of a line that lies between, and includes, its two distinct endpoints p and q . A line segment has finite length.
Since the end points of a 1-disc are distinct, they are points of a 0-sphere the boundary of a 1-disc is a 0-sphere S 0.
We can glue two 1-discs along their S 0 boundaries to obtain a one-sphere S 1 (Figure ): Starting with two 1-discs, say [ p , q ] and [ p , q ], we first flex each of these discs into a semicircle, then we join the two semicircles by gluing p to p , and, q to q . After the gluing we have p = p and q = q as illustrated, and the result is a one-sphere S 1.
Fig. 1.5
Two 1-discs glued at their S 0 boundaries yield S 1.
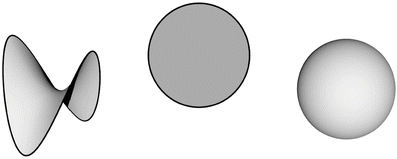
Next, we step up to the two-dimensional case. The simplest examples of two-dimensional objects are planes and either curved or flat surfaces:
From left-to-right we see a saddle surface (horse saddle), a 2-disc (circular flat area bounded by a circle S 1), and a 2-sphere (seamless inflated balloon).
We can also glue two 2-discs along their S 1 boundaries to obtain a 2-sphere S 2 (Figure ): Starting with two 2-discs, we first flex each of these discs into a hemisphere, then we join the two hemispheres by gluing their S 1 boundaries. After the gluing, the two S 1 boundaries are equal as illustrated, and the result is a two-sphere S 2.