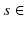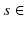Introduction: How Nature Works
Borrowing from nature has become a well-established practice in computing. The reasons for this are easy to understand. Computing has to deal with increasingly complex problems where traditional methods often do not work well. Natural systems have evolved ways to solve such problems. Methods borrowed from nature include both ways to represent and model systems, such as cellular automata or neural networks, and procedures to solve complex problems.
The motivation for basing algorithms on nature is that the natural processes concerned are known to produce desirable results, such as finding an optimal value of some feature. This observation has inspired many algorithms based on nature. Despite their effectiveness, methods modelled on nature have often been treated with suspicion. Traditional mathematical methods, such as linear programming, are based on well-known theoretical foundations. So their interpretation, and their limitations, can be tested analytically. In contrast, nature-based methods are ad hoc heuristics based on phenomena whose properties are not always understood, even by biology.
The above issues raise a need to identify theoretical foundations to underpin nature-based algorithms. To address this need, we set out to do the following in this account. First, we identify features that are common to many nature-inspired algorithms and show how these are described by a formal model that explains why the algorithms work. Secondly, we describe three frameworks for describing nature-inspired algorithms and their operation. Finally, we discuss some deeper issues about the differences between natural processes and methods based on them. This includes both the danger of simplifying nature and further lessons we can derive from the way processes actually work in nature.
The Nature of Nature
Many natural processes have inspired optimization algorithms. However, most of them share a common underlying model, which reveals how they work. We begin with a simple example that captures the main features. The great deluge algorithm (GDA) is based on the idea of an agent moving about in a landscape, and the landscape is in the process of being flooded []. Initially, the agent can wander freely anywhere in the landscape. However, the rising water level prevents entry into low-lying areas. These areas expand and coalesce, until eventually the agent is trapped on a single peak, after which all it can do is to climb to the top of that peak.
An optimization algorithm based on GDA interprets model parameters as coordinates in an N -dimensional landscape. The object variable, which is to be maximized, is treated as elevation. The flood level then becomes a constraining lower limit on the object function, which is gradually raised. The agent is a model that performs a random walk through the solution space, rejecting any move to a region where the object function falls below the flood level. The algorithm terminates when the agent can no longer find anywhere above flood level. An important feature of the algorithm is a transition from global search in which it can move freely anywhere, to local search, in which it is constrained to a local neighbourhood.
In the great deluge algorithm, the agent continues to take a random walk within the local region in which it is confined and is forced to move uphill as rising water level progressively shrinks the size of the region. A more efficient approach to this final search is hill climbing. Based on the analogy with a mountaineer ascending a mountain, in hill climbing the agent does not wander at random, but moves uphill on every step, until it reaches a local peak.
By mimicking natural processes, nature-inspired algorithms (NIAs) provide ways to find a target by navigating a search through a network of possibilities. The manner of these searches sometimes reveals deep similarities between completely different systems. Other algorithms, for example simulated annealing (see Sect. ) and the great deluge algorithm use analogues with natural processes to manage a switch from what is initially a global search to a local search in their final stages.
We can see another example of deep similarity if we compare the gravitational search algorithm (GSA) []. Both involve attraction between potential solutions. Initially, these are scattered across a search space, and weaker solutions move towards better ones. GSA represents solutions as objects in an N -dimensional space. Their locations are given by values of N parameters, and their masses are values of the object function. Gravitational attraction draws the objects towards each other, with smaller masses moving closer to larger ones. The firefly algorithm mimics the flashing behaviour of fireflies. As in GSA, the fireflies are scattered over an N -dimensional space. The brightness of a fireflys flashes corresponds to the quality of its solution. Fireflies are attracted to others with brighter flashes, but brightness decreases with distance.
The simple models discussed above capture features that are present in many nature-inspired algorithms (NIAs). The procedures are characterized as a search through a space defined by values of the variables, with a transition from a global search to a local search. For optimization problems, the idea of a search space leads to the concept of a fitness landscape.
2.1 Fitness Landscape
The notion of a fitness landscape is an abstraction developed in evolutionary theory and borrowed by the optimization community to explain the relationship between an optimization problem and the search algorithm. For optimization problems, many NIAs provide ways to search the fitness landscape.
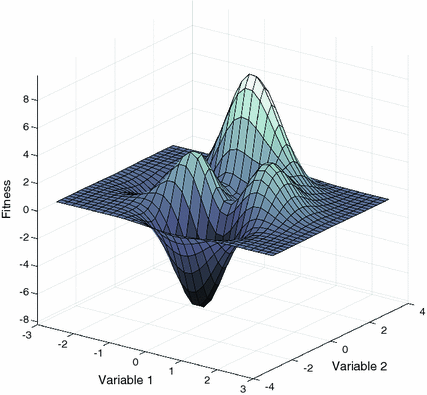
Fig. 1
An example of a fitness landscape of a maximization problem. Note the two small peaks (local optima) in front of the large one (global optimum)
Formally, a fitness landscape has the following components: (i) a set of possible solutions s , also known as the search space, (ii) the distance (neighbourhood) operator, which assigns each solution