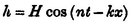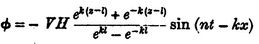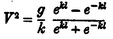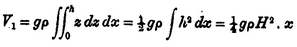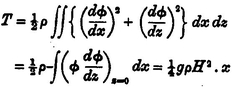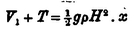APPENDIX.
ON PROGRESSIVE WAVES .
From the Proceedings of the London Mathematical Society, Vol. IX., p. 21, 1877.
It has often been remarked that, when a group of waves advances into still water, the velocity of the group is less than that of the individual waves of which it is composed ; the waves appear to advance through the group, dying away as they approach its anterior limit. This phenomenon was, I believe, first explained by Stokes, who regarded the group as formed by the Superposition of two infinite trains of waves, of equal amplitudes and of nearly equal wave-lengths, advancing in the same direction. My attention was called to the subject about two years since by Mr Froude, and the same explanation then occurred to me independently. In my book on the Theory of Sound (191), I have considered the question more generally, and have shewn that, if V be the velocity of propagation of any kind of waves whose wave-length is , and k = 2/, then U, the velocity of a group composed of a great number of waves, and moving into an undisturbed part of the medium, is expressed by
or, as we may also write it,
Thus, if
In fact, if the two infinite trains be represented by cos k ( V t-x ) and cos k ( V t x ), their resultant is represented by
cos k ( Vt - x ) + cos k ( V t - x ),
which is equal to
If k - k , V V be small, we have a train of waves whose amplitude varies slowly from one point to another between the limits 0 and 2, forming a series of groups separated from one another by regions comparatively free from disturbance. The position at time t of the middle of that group, which was initially at the origin, is given by
( k V kV ) t ( k k ) 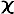 = 0,
= 0,
which shews that the velocity of the group is ( k V kV )( k k). In the limit, when the number of waves in each group is indefinitely great, this result coincides with (1).
The following particular cases are worth notice, and are here tabu lated for convenience of comparison:
| V , | U = 0, | Reynolds disconnected pendulums. |
V  , , , , | U = 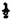 , V , V | Deep-water gravity waves. |
| V x 0, | U = V , | Arial waves, &c. |
V 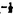 , , | U = 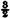 V , V , | Capillary water waves. |
| V 1 | U = 2 V , | Flexural waves. |
The capillary water waves are those whose wave-length is so small that the force of restitution due to capillarity largely exceeds that due to gravity. Their theory has been given by Thomson (Phil. Mag., Nov. 1871). The flexural waves, for which U = 2V, are those corresponding to the bending of an elastic rod or plate (Theory of Sound, 191).
In a paper read at the Plymouth meeting of the British Association (afterwards printed in Nature, Aug. 23, 1877), Prof. Osborne Reynolds gave a dynamical explanation of the fact that a group of deep-water waves advances with only half the rapidity of the individual waves. It appears that the energy propagated across any point, when a train of waves is passing, is only one-half of the energy necessary to supply the waves which pass in the same time, so that, if the train of waves be limited, it is impossible that its front can be propagated with the full velocity of the waves, because this would imply the acquisition of more energy than can in fact be supplied. Prof. Reynolds did not contemplate the cases where more energy is propagated than corresponds to the waves passing in the same time ; but his argument, applied conversely to the results already given, shews that such cases must exist. The ratio of the energy propagated to that of the passing waves is U : V ; thus the energy propagated in the unit time is U : V of that existing in a length V , or U times that existing in the unit length. Accordingly
Energy propagated in unit time : Energy contained (on an average) in unit length = d ( kV ) : dk , by (1).
As an example, I will take the case of small irrotational waves in water of finite depth l . If z be measured downwards from the surface, and the elevation ( h ) of the wave be denoted by
in which n = kV , the corresponding velocity-potential () is
This value of satisfies the general differential equation for irrotational motion 2 = 0), makes the vertical velocity d / dz zero when z = l , and dh/dt when z = 0. The velocity of propagation is given by
We may now calculate the energy contained in a length x , which is supposed to include so great a number of waves that fractional parts may be left out of account.
For the potential energy we have
For the kinetic energy,
by (5) and (6). If, in accordance with the argument advanced at the end of this paper, the equality of V 1 and T be assumed, the value of the velocity of propagation follows from the present expressions. The whole energy in the waves occupying a length x is therefore (for each unit of breadth)
H denoting the maximum elevation.
We have next to calculate the energy propagated in time t across a plane for which x is constant, or, in other words, the work ( W ) that must be done in order to sustain the motion of the plane (considered as a flexible lamina) in the face of the fluid pressures acting upon the front of it. The variable part of the pressure ( p ), at depth z , is given by












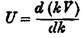
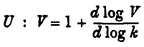

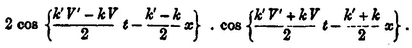
 = 0,
= 0, , ,
, , , V
, V ,
,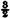 V ,
V ,