Quantification
Illustrations from the Creator of Secrets in Plain Sight
by Scott Onstott
Copyright 2014 SIPS Productions Inc.
Introduction
This book of illustrations documents my continuing efforts to understand the universe and our place in it and at the same time is an attempt to understand the self and the universe within. I experienced a creative outpouring in the first 3 months of 2014 and the overwhelming majority of these illustrations are from that period. However, I was also inspired to include a few illustrations I made from as far back as 3 years ago to round out the collection.
More than a third of the illustrations are of the Great Pyramidits geometry and location are fascinating! Ive made a number of unusual comparisons between ancient and modern structures, sacred sites, the Earth, Moon, Sun, the human body and much more besides.
Many of the illustrations reveal uncanny connections that will probably get you wondering and contemplating. I hope that some of these might catalyze you into doing your own research, asking philosophical questions, and examining your own experience. Never before has humanity had such opportunity at our fingertips as we now enjoy with the Internet.
I designed this book so that illustrations logically flow in linear order, but feel free to jump around and examine any page that you happen to come to and see where it takes you. Many of my best discoveries have been made by following trails of synchronicity.
Scott Onstott
March 2014
Cortes Island, British Columbia
Canada

Enter the Matrix
Great complexity can arise from simple beginnings. Imagine a light, a camera and a dodecahedron. This image was made by placing a virtual camera inside a reflective dodecahedral lattice with a single, omnidirectional light source in the center. Each ray that entered the camera lens was traced backwards, through many reflections, back to the light source to determine each pixels color through its history of interaction. That is how the ray-tracing algorithm produced this staggering complexity from within the humble dodecahedron.
The dodecahedron is one of five Platonic solids. Plato himself claimed the dodecahedron, was used for the universe as a whole in the Timaeus. Astrophysicist Jean-Pierre Luminet of the Observatoire de Paris and colleagues suggested that the universe is finite and shaped like a dodecahedron attached to itself by each pair of opposite faces, because this mirrored shape best fits the cosmic microwave background radiation data recorded by satellite.[1]
The Mystery of 273
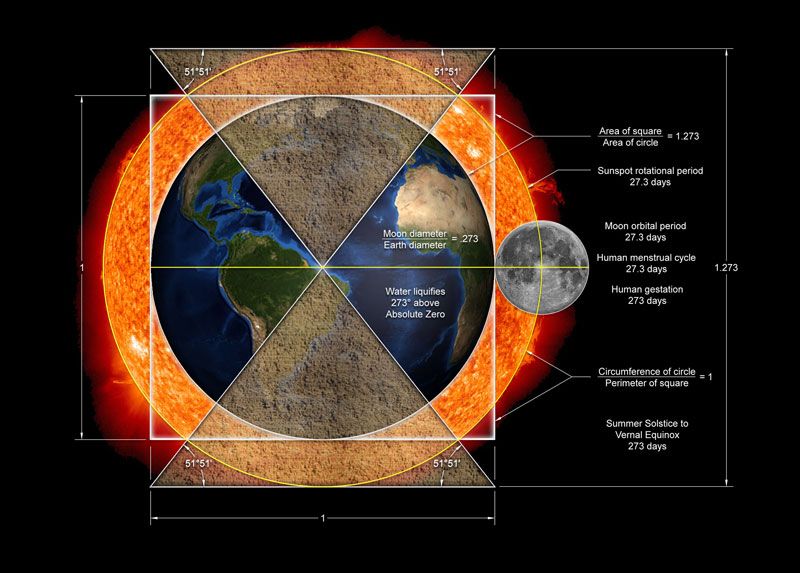
Since ancient times geometers and philosophers have sought to square the circleto draw a square whose perimeter equals the circumference of a circle. The square represents the built human worldwith right angles and linear distances it is easily measured and rationalized. The circle, being an infinite number of points equidistant from a center, represents the transcendental realm governed by . Drawing a square commensurate with such a circle mirrors humankinds efforts to transcend the rational and yet still include it in a higher level.
The relationship of the Great Pyramids base to height remarkably squares the circle. If the pyramids base width is 1, then its height is the radius of a circle whose diameter is 1.273. The area of a square divided by the area of its inscribed circle is also 1.273. The Moons diameter divided by the Earths diameter equals .273. Sunspots revolve about the Suns surface in 27.3 days, the Moon orbits the Earth in 27.3 days, the human menstruation cycle averages 27.3 days and women carry infants within for 273 days. Water changes phase at 273K and there are 273 days from the summer solstice to the vernal equinox. The fact that all of these phenomena converge on 273 is a mystery.
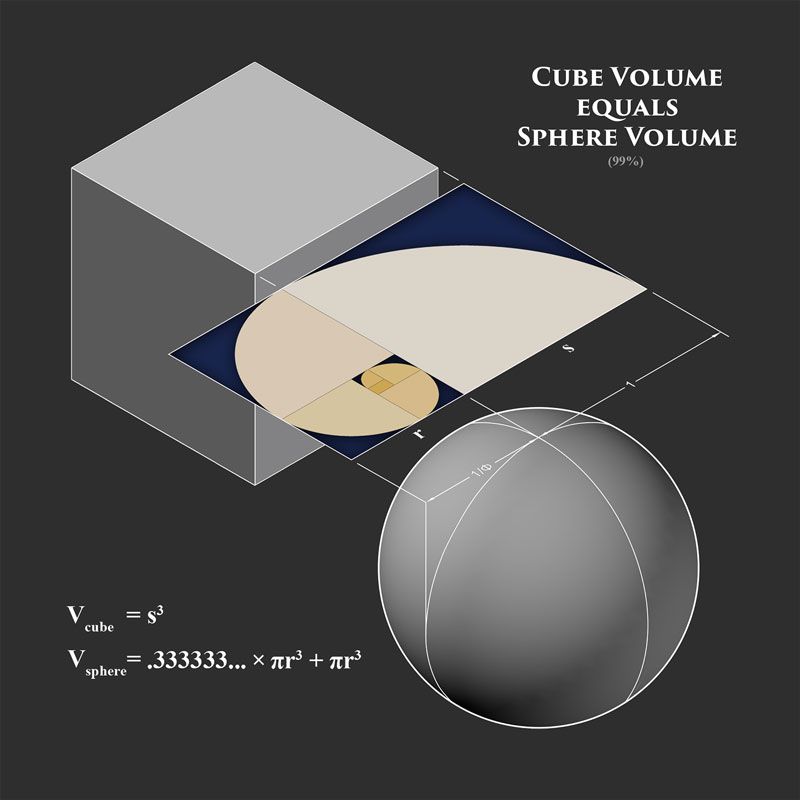
Cubing the Sphere
In ancient times generations of geometers strove to square the circle, but today I ponder other possibilities for building a symbolic bridge between the finite and the infinite. As an extension of the square into the third dimension, I take the cube as a metaphor for embodiment itself. Like the circle, the sphere is defined as an infinite number of points equidistant from a center, but the sphere expands into an additional dimension. Imagine an infinite space seething with limitless potential. You enter this matrix as a point of awareness. To explore this space you move a distance and stop. Your next logical step is to explore the infinity of points equidistant from your initial locationdoing so you actually trace the surface of a hyperdimensional sphere. The three-dimensional sphere is a stepped down metaphor for awareness, for spirit, for you who are reading these words. By cubing the sphere we attempt to ground the infinite within the finite, symbolically embodying spirit in matter. The key to this movement is the golden ratio . I have rewritten the standard formula for the volume of a sphere (V = 4/3 x r3) as V = .333333... x r3 + r3 in order to highlight its relationship with the infinite repetition of 3s.
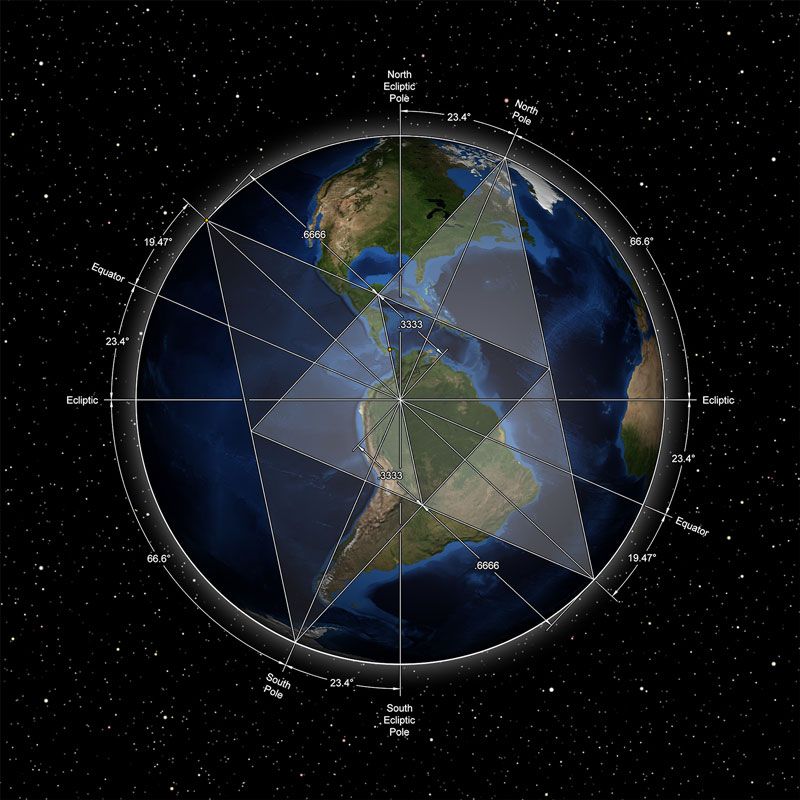
Earthstar
The Earth is shown here circumscribing two tetrahedrons, the simplest of all Platonic solids. Plato equated the tetrahedron to the most primal elementfire. The Island of Hawaii is indicated at the tip of a tetrahedron on the upper left, formed from five massive shield volcanos located 19.47 north of the equator. The Big Island is Earths tallest mountain when measured from the sea floor, taller than Mount Everest is above sea level. Richard Hoagland discovered this connection and proposed a theory of hyperdimensional physics to explain it.[2]
If the radius of the Earth is taken to be 1, then the point of each tetrahedron extends .6666... of the distance to the opposite tetrahedron. I find it interesting that the angle from the North Pole to the ecliptic measures 66.6 and that the Earth orbits at a velocity of 66660 miles/hour. In addition, recent high precision experiments reveal the value of the gravitational constant G = 6.666 x 10-11 N (m/kg)2 is within the uncertainty of the measurements.[3] Its intriguing also that the sine of 19.47= .3333.

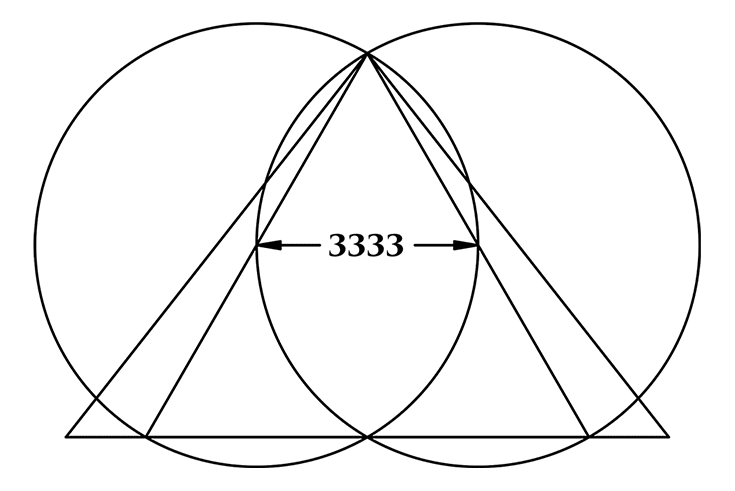
Triangulating the Circle
This illustrates a method of triangulating the circle, such that the perimeter of the isosceles triangle, shown in magenta, equals the circumference of the green circle (with 99.8% accuracy). I read about this geometry in Geneset by David Wood and Ian Campbell. They discovered the fascinating connection between the geometry of the 15-pointed star and the same isosceles triangle in their analysis of the structured landscape surrounding Rennes-le-Chateau. John Martineaus




















