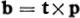DIFFERENTIAL
GEOMETRY BY
ERWIN KREYSZIG DOVER PUBLICATIONS, INC.
New York This Dover edition, first published in 1991, is an unabridged republication of the 1963 printing of the work first published by The University of Toronto Press, Toronto, in 1959 as No. 11 in their series, Mathematical Expositions. Library of Congress Cataloging-in-Publication Data Kreyszig, Erwin. Differential geometry / Erwin Kreyszig. p. Reprint. Reprint.
Originally published: Toronto: University of Toronto Press, 1959. (Mathematical expositions; no. 11) Includes bibliographical references and index. ISBN-13: 978-0-486-66721-8 (pbk.) ISBN-10: 0-486-66721-9 (pbk.) 1. Geometry, Differential. Title. Title.
QA641.K883 1991
516.36dc20 91-14321
CIP Manufactured in the United States by Courier Corporation 66721910 www.doverpublications.com DEDICATED TO PROFESSOR S. BERGMAN Stanford UniversityPREFACE THIS book provides an introduction to the differential geometry of curves and surfaces in three-dimensional Euclidean space. We first consider some basic concepts and facts of analytic geometry which will be useful for later investigations. The theory of space curves is presented in the second chapter. We then proceed to the foundations of the theory of surfaces. Problems closely related to the first and second fundamental forms are considered in the third and fourth chapter..
In the theory of surfaces we make full use of the tensor calculus, which is developed as needed, cf.. He will perceive that the tensor method is helpful in achieving a simplification of the analytic formalism of many investigations. Hence tensors are important tools in modern differential geometry. The presentation in this book may also be considered as a preparation for the Riemannian geometry of n dimensions. As is well known, tensors are of increasing importance not only in mathematics, but also in the application of mathematics to physics and engineering. Since the problems treated in differential geometry by means of tensor calculus are relatively perspicuous, they enable us to understand not only the formalism but also the nature and essential background of this calculus.
The student will thus gain by being able to apply his knowledge of tensors to fields other than that of differential geometry. In using tensor calculus one should never forget that the purpose of this calculus lies in its applications to certain problems; it is a tool only, albeit a very powerful one. We should mention that many of the topics considered in this book can also be investigated by means of outer differential forms. Cf. E. Cart an, Les Systmes diffrentiels extrieurs et leurs applications gomtriques (Paris, 1945), W.
Blaschke, Einfhrung in die Differentialgeometrie (Berlin, 1950). In writing this book, the experiences which I gained during the period of personal co-operation with Professor H. Behnke (University of Mnster in Westphalia), as well as his printed lecture notes on differential geometry, were of help to me. I have tried to present the whole subject-matter in the simplest possible form consistent with the needs of mathematical rigour, and to convey a clear idea of the geometric significance of the different concepts, methods, and results. For this reason also, numerous figures and examples are included in the text. In order to lessen the readers difficulties, especially for those who are approaching differential geometry for the first time, the discussion is relatively detailed.
The selection of topics included in this book has been made with great care, consideration being given to the didactic point of view as well as the theoretical and practical importance of the different aspects of the subject. Problems are to be found at the end of almost every section, and the solutions are listed at the end of the book. These exercises should help the reader to become familiar with the material presented in the text and, what is more important, to get acquainted with the manner of reasoning in differential geometry. Differential geometry has various relations to other fields of mathematics. Besides the calculus other branches, such as function theory, the calculus of variations, and the theory of differential equations, are also basically important in differential geometry. On the other hand, differential geometry is an essential part of the foundations of some applied sciences, for instance physics, geodesy, and geography.
Differential geometry has therefore what we may call a general character; I have tried to stress this point of view in connexion with several topics. This book is a free translation of my Differentialgeometrie which appeared in the series Mathematik und ihre Anwendungen in Physik und Technik (Mathematics and its applications to physics and technical science) (Series A, vol. 25) of the Akademische Verlagsgesellschaft, Geest und Portig, Leipzig, Germany. Some minor changes have been made in the course of translation. Professor H. Behnke (University of Mnster) and Professor H.
Graf (Technical University of Darmstadt) have made valuable suggestions to me. Professor S. Bergman (Stanford University) and Professor E. Ullrich (University of Giessen) have checked , respectively. Professor C. Loewner (Stanford University), Professor M.
Riesz (University of Lund), Professor H. S. M. Ooxeter (University of Toronto), Professor P. Scherk (University of Saskatchewan), Professor M. Barner (Technical University of Karlsruhe), and Professor 0.
Biberstein (University of Ottawa) have read the manuscript carefully, and I have obtained valuable suggestions from all of them in the course of numerous personal discussions. The translated manuscript has been checked by Professor H. S. M. Coxeter, Professor G. D. D.
Duff (University of Toronto), Professor J. T. Duprat (University of Ottawa), Professor R. C. Fisher (Ohio State University, Columbus), and Professor L. Sauv (St.
Patricks College, Ottawa). I wish to express my gratitude to all of them and also to the University of Toronto Press, for their efficient co-operation. E. K. CONTENTS I PRELIMINARIES 1. Notation. In this section the meaning of some symbols occurring very frequently in our text will be explained and the page on which these symbols are introduced for the first time indicated.
The reader will find another index of definitions, formulae, and theorems at the end of this book.
| x1, x2, x3: Cartesian coordinates in three-dimensional Euclidean space R3. |
| Bold-face letters a, y, etc.: Vectors in space R3; the components of these vectors will be denoted by a1, a2, a3; y1, y2, y3, etc. |
s arc length of a curve. Derivatives with respect to s will be denoted by dots, e.g. 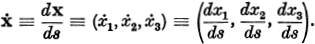 An arbitrary parameter figuring in the representation of a curve will usually be denoted by t. An arbitrary parameter figuring in the representation of a curve will usually be denoted by t. Derivatives with respect to t will be characterized by primes, e.g. 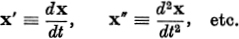 |
 unit tangent vector of a curve C: x(s). unit tangent vector of a curve C: x(s). |
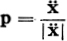 unit principal normal vector of that curve. unit principal normal vector of that curve. |
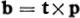 |
Next page











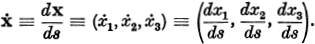 An arbitrary parameter figuring in the representation of a curve will usually be denoted by t.
An arbitrary parameter figuring in the representation of a curve will usually be denoted by t. 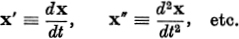
 unit tangent vector of a curve C: x(s).
unit tangent vector of a curve C: x(s).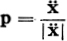 unit principal normal vector of that curve.
unit principal normal vector of that curve.