The Math Handbook
Everyday Math Made Simple
Richard Elwes
Contents
Introduction
I was never any good at mathematics.
I must have heard this sentence from a thousand different people.
I cannot dispute that it may be true: people do have different strengths and weaknesses, different interests and priorities, different opportunities and obstacles. But, all the same, an understanding of mathematics is not something anyone is born with, not even Pythagoras himself. Like all other skills, from portraiture to computer programming, from knitting to playing cricket, mathematics can only be developed through practice, that is to say through actually doing it.
Nor, in this age, is mathematics something anyone can afford to ignore. Few people stop to worry whether they are good at talking or good at shopping. Abilities may indeed vary, but generally talking and shopping are unavoidable parts of life. And so it is with mathematics. Rather than trying to hide from it, how about meeting it head on and becoming good at it?
Sounds intimidating? Dont panic! The good news is that just a handful of central ideas and techniques can carry you a very long way. So, I am pleased to present this book: a no-nonsense guide to the essentials of the subject, especially written for anyone who was never any good at mathematics. Maybe not, but its not too late!
Before we get underway, heres a final word on philosophy. Mathematical education is split between two rival camps. Traditionalists brandish rusty compasses and dusty books of log tables, while modernists drop fashionable buzzwords like chunking and talk about the number line. This book has no loyalty to either group. I have simply taken the concepts I consider most important, and illustrated them as clearly and straightforwardly as I can.
Many of the ideas are as ancient as the pyramids, though some have a more recent heritage. Sometimes a modern presentation can bring a fresh clarity to a tired subject; in other cases, the old tried and tested methods are the best.
Richard Elwes
The language of mathematics
Writing mathematics
Understanding what the various mathematical symbols mean, and how to use them
Using BEDMAS to help with calculations

Lets begin with one of the commonest questions in any mathematics class: Cant I just use a calculator? The answer is of course you can! This book is not selling a puritanical brand of mathematics, where everything must be done laboriously by hand, and all help is turned down. You are welcome to use a calculator for arithmetic, just as you can use a word-processor for writing text. But handwriting is an essential skill, even in todays hi-tech world. You can use a dictionary or a spell-checker too. All the same, isnt it a good idea to have a reasonable grasp of basic spelling?
There may be times when you dont have a calculator or a computer to hand. You dont want to be completely lost without it! Nor do you want to have to consult it every time a few numbers need to be added together. After all, you dont get out your dictionary every time you want to write a simple phrase.
So, no, I dont want you to throw away your calculator. But I would like to change the way you think about it. See it as a labor saving device, something to speed up calculations, a provider of handy shortcuts.
The way I dont want you to see it is as a mysterious black box which performs near-magical feats that you alone could never hope to do. Some of the quizzes will show this icon  , which asks you to have a go without a calculator. This is just for practice, rather than being a point of principle!
, which asks you to have a go without a calculator. This is just for practice, rather than being a point of principle!
Signs and symbols
Mathematics has its own physical toolbox, full of calculators, compasses and protractors. We shall meet these in later chapters. Mathematics also comes with an impressive lexicon of terms, from radii to logarithms, which we shall also get to know and love in the pages ahead.
Perhaps the first barrier to mathematics, though, comes before these: it is the library of signs and symbols that are used. Most obviously, there are the symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. It is interesting that once we get to the number ten there is not a new symbol. Instead, the symbols for 0 and 1 are recycled and combined to produce the name 10. Instead of having one symbol alone, we now have two symbols arranged in two columns. Which column the symbol is in carries just as much information as the symbol itself: the 1 in 13 does not only mean one, it means one ten. This method of representing numbers in columns is at the heart of the decimal system: the modern way of representing numbers. It is so familiar that we might not realize what an ingenious and efficient system it is. Any number whatsoever can be written using only the ten symbols 09. It is easy to read too: you dont have to stop and wonder how much 41 is.
This way of writing numbers has major consequences for the things that we do with them. The best methods for addition, subtraction, multiplication and division are based around understanding how the columns affect each other. We will explore these in depth in the coming chapters.
There are many other symbols in mathematics besides numbers themselves. To start with, there are the four representing basic arithmetical procedures: +, , , . In fact there are other symbols which mean the same things. In many situations, scientists prefer a dot, or even nothing at all, to indicate multiplication. So, in algebra, both ab and a b, mean the same as a b, as we shall see later. Similarly, division is just as commonly expressed by 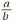 as by a b.
as by a b.
This use of letters is perhaps the greatest barrier to mathematics. How can you multiply and divide letters? (And why would you want to?) These are fair questions, which we shall save until later.
Writing mathematics
Here is another common question:

What is the point of writing out mathematics in a longwinded fashion? Surely all that matters is the final answer?
The answer is no! Of course, the right answer is important. I might even agree that it is usually the most important thing. But it is certainly not the only important thing. Why not? Because you will have a much better chance of reliably arriving at the right answer if you are in command of the reasoning that leads you there. And the best way of ensuring that is to write out the intermediate steps, as clearly and accurately as possible.
Writing out mathematics has two purposes. Firstly it is to guide and illuminate your own thought-processes. You can only write things out clearly if you are thinking about them clearly, and it is this clarity of thought that is the ultimate aim. The second purpose is the same as for almost any other form of writing: it is a form of communication with another human being. I suggest that you work under the assumption that someone will be along shortly to read your mathematics (whether or not this is actually true). Will they be able to tell what you are doing? Or is it a jumble of symbols, comprehensible only to you?









 , which asks you to have a go without a calculator. This is just for practice, rather than being a point of principle!
, which asks you to have a go without a calculator. This is just for practice, rather than being a point of principle!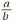 as by a b.
as by a b.