J. Murray Barbour - Tuning and Temperament: A Historical Survey

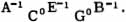
Fludds Monochord, with Pythagorean Tuning and Associated Symbolism Reproduced by courtesy of the Library of Cornell University

A Historical Survey

J. Murray Barbour

Dover Publications, Inc.

Mineola, New York

Bibliographical Note

This Dover edition, first published in 2004, is an unabridged republication of the work originally published by Michigan State College Press, East Lansing, 1951. The frontispiece has been printed on the inside of the front cover and as a result the present volume begins on page iii. Nothing has been omitted from this edition.

Library of Congress Cataloging-in-Publication Data

Barbour, J. Murray (James Murray), 1897

Tuning and temperament: a historical survey / J. Murray Barbour.

p. cm.

Originally published: East Lansing: Michigan State Press, 1951.

Includes bibliographical references (p.).

ISBN 0-486-43406-0 (pbk.)

1. Tuning. 2. Musical temperament. I. Title.

ML3809.B234 2004

784.1928dc22

2004043835

Manufactured in the United States by Courier Corporation

43406004

www.doverpublications.com

This book is based upon my unpublished Cornell dissertation, Equal Temperament: Its History from Ramis (1482) to Rameau (1737) , Ithaca, 1932. As the title indicates, the emphasis in the dissertation was upon individual writers. In the present work the emphasis is on the theories rather than on their promulgators. Since a great many tuning systems are discussed, a separate chapter is devoted to each of the principal varieties of tuning, with subsidiary divisions wherever necessary. Even so, the whole subject is so complex that it seemed best that these chapters be preceded by a running account (with a minimum of mathematics) of the entire history of tuning and temperament. also contains the principal account of the Pythagorean timing, for it is unnecessary to spend a chapter upon a tuning system that exists in one form only.

Most technical terms will be defined when they first occur, as well as in the Glossary, but a few of these terms should be defined immediately. Of small intervals arising from tuning, the comma is the most familiar. The ordinary (syntonic or Ptolemaic) comma is the interval between a just major third, with ratio 5:4, and a Pythagorean ditone or major third, with ratio 81:64. The ratio of the comma (the ratio of an interval is obtained by dividing the ratio of the higher pitch by that of the lower) is 81:80.

The Pythagorean (ditonic) comma is the interval between six tones, with ratio 531441:262144, and the pure octave, with ratio 2:1. Thus its ratio is 531441:524288, which is approximately 74:73. The ditonic comma is about 12/11 as large as the syntonic comma. In general, when the word comma is used without qualification, the syntonic comma is meant.

There is necessarily some elasticity in the manner in which the different tuning systems are presented in the following chapters. Sometimes a writer has described the construction of a monochord, a note at a time. That can be set down easily in the form of ratios. More often he has expressed his monochord as a series of string-lengths, with a convenient length for the fundamental. (Except in the immediate past, the use of vibration numbers, inversely proportional to the string-lengths, has been so rare that it can be ignored.) Or he may speak of there being so many pure fifths, and other fifths flattened by a fractional part of the comma. Such systems could be transformed into equivalent string-lengths, but this has not been done in this book when the original writer had not done so.

Systems with intervals altered by parts of a comma can be shown without difficulty in terms of Ellis logarithmic unit called the cent, the hundredth part of an equally tempered semitone, or 1/1200 part of an octave.* Since the ratio of the octave is 2:1, the cent is 21/1200. As a matter of fact, such eighteenth century writers on temperament as Neidhardt and Marpurg had a tuning unit very similar to the cent: the twelfth part of the ditonic comma, which they used, is 2 cents, thus making the octave contain 600 parts instead of 1200.

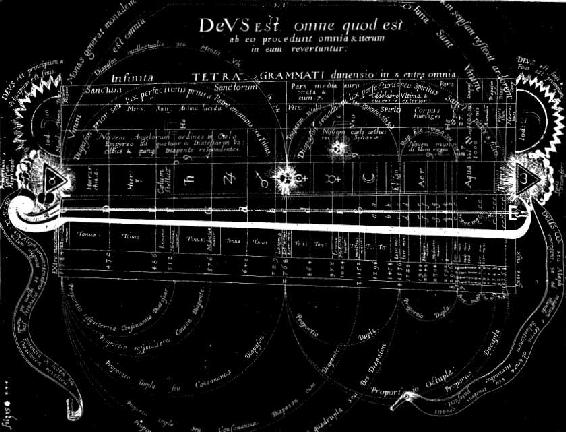
The systems originally expressed in string-lengths or ratios may be translated into cents also, although with greater difficulty. They have been so expressed in the tables of this book, in the belief that the cents representation is the most convenient way of affording comparisons between systems. In systems where it was thought they would help to clarify the picture, exponents have been attached to the names of the notes. With this method, devised by Eitz, all notes joined by pure fifths have the same exponent. Since the fundamental has a zero exponent, all the notes of the Pythagorean tuning have zero exponents. The exponent -1 is attached to notes a comma lower than those with zero exponents, i.e., to those forming pure thirds above those in the zero series. Thus in just intonation the notes forming a major third would be C0-E_1, etc. Similarly, notes that are pure thirds lower than notes already in the system have exponents which are greater by one than those of the higher notes. This use of exponents is especially advantageous in comparing various systems of just intonation (see ). It may be used also, with fractional exponents, for the different varieties of the meantone temperament. If the fifth C-G, for example, is tempered by 1/4 comma, these notes would be labeled C0 and G-1/4.

A device related to the use of integral exponents for the notes in just intonation is the arrangement of such notes to show their harmonic relationships. Here, all notes that are related by fifths, i.e., that have the same exponent, lie on the same horizontal line, while their pure major thirds lie in a parallel line above them, each forming a 45 angle with the related note below. Since the pure minor thirds below the original notes are lower by a fifth than the major thirds above them, they will lie in the same higher line, but will form 135 angles with the original notes. For example:

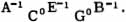
This arrangement is especially good for showing extensions of just intonation with more than twelve notes in the octave, and it is used for that purpose only in this book (see ).

It is desirable to have some method of evaluating the various tuning systems. Since equal temperament is the ideal system of twelve notes if modulations are to be made freely to every key, the semitone of equal temperament, 100 cents, is taken as the ideal, from which the deviation of each semitone, as C-C#, C#-D, D-Eb, etc., is calculated in cents. These deviations are then added and the sum divided by twelve to find the mean deviation (M.D.) in cents. The standard deviation (S.D.) is found in the usual manner, by taking the root-mean-square.

It should be added that there may be criteria for excellence in a tuning system other than its closeness to equal temperament. For example, if no notes beyond Eb or G# are used in the music to be performed and if the greatest consonance is desired for the notes that are used, then probably the 1/5 comma variety of mean - tone temperament would be the ideal, since its fifths and thirds are altered equally, the fifths being 1/5 comma flat and its thirds 1/5 comma sharp. If keys beyond two flats or three sharps are to be touched upon occasionally, but if it is considered desirable to have the greatest consonance in the key of C and the least in the key of Gb, then our Temperament by Regularly Varied Fifths would be the best. This is a matter that is discussed in detail at the end of , but it should be mentioned now.