THE
LITTLE
BOOK OF
SCIENTIFIC
PRINCIPLES,
THEORIES
& THINGS
SURENDRA VERMA
First published in Australia in 2005 by
Reed New Holland
an imprint of New Holland Publishers (Australia) Pty Ltd
Sydney Auckland London Cape Town
www.newholland.com.au
14 Aquatic Drive Frenchs Forest NSW 2086 Australia
218 Lake Road Northcote Auckland New Zealand
86 Edgware Road London W2 2EA United Kingdom
80 McKenzie Street Cape Town 8001 South Africa
Copyright 2005 in text: Surendra Verma
Copyright 2005 New Holland Publishers (Australia) Pty Ltd
All rights reserved. No part of this publication may be reproduced, stored in a retrieval system or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, without the prior written permission of the publishers and copyright holders.
National Library of Australia Cataloguing-in-Publication Data:
ISBN 1 877069 20 5
e-ISBN 9781921655425
This book introduces more than 200 laws, principles, theories, hypotheses, rules, postulates, theorems, experiments, models, systems, paradoxes, equations, constants and other ideas that form the foundations of science. (The meanings of the terms law, principle etc. are explained in the appendix under The Scientific Method, on p. 202.)
The entries are arranged in chronological order. The popular name of the idea is used; in most cases it includes the name of the person who formulated the idea, for example, Archimedes Principle.
You may read the book in order, or dip into it at random. Each entry is complete in itself, but cross-references are provided where appropriate. The key on the opposite page explains the order of information in each entry.
The comprehensive index will help you to find the ideas covered in this book. Main entries appear in bold in the index, as do some additional terms/ideas (also bolded in text).
Abbreviations used c. circa (meaning approximately) b. born p. page pp. pages |
Sixth
century
BC GREECE | Pythagoras Theorem Pythagoras (c. 580 c. 500 BC ) |
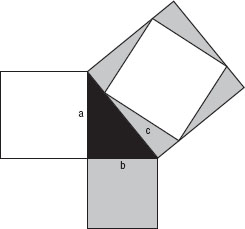
In a right-angled triangle, the square on the hypotenuse is the sum of the squares on the other two sides. |
T he theorem can also be written as a general law: a2 + b2 = c2 , where c is the length of the hypotenuse of a right-angled triangle, and a and b the lengths of other two sides. Pythagoras theorem is a starting point for trigonometry, which has many practical applications such as calculating the height of mountains and measuring distances.
Legend has it that Pythagoras was once walking on the chequered floor of a temple in Egypt. The floor had alternatively coloured squares. The shadow of pillars was falling obliquely across these squares. The shadows and squares suggested different geometrical patterns. His interest in geometry led him to study these patterns from different angles and then to the discovery of the proof of the theorem.
Pythagoras was the first to prove the relationship between the sides of a right-angled triangle, but he did not discover itit was known to Babylonians for nearly 1000 years before him. He was also the first to discover that the Earth was a sphere. This discovery was confirmed by Eratosthenes (p. 15).
The square on the hypotenuse of the right-angled black triangle is equal to the sum of the squares on the other two sides. (The white squares are the same size; the four shaded pieces make the shaded square.)
Fifth
century
BC GREECE | Zenos Paradoxes Zeno (lived c. 450 BC ) |
Motion is an illusion. |
Z eno devised four paradoxes, all of which seemed to prove the impossibility of motion.
The most famous of Zenos paradoxes is that of Achilles and the tortoise: the faster of two runners can never overtake the slower, if the slower is given any start at all. Suppose Achilles, a hero of the Trojan War, reputed to be the swiftest runner ever known, can run ten times as fast as a tortoise and the tortoise has a 100-metre head start. When Achilles has run 100 metres the tortoise will have crawled 10 metres, and so will be 10 metres in front, and so on. Mathematically, Achilles can only keep getting nearer and nearer to the tortoise, but he can never overtake it.
Zenos paradoxes were based on the false assumption that space and time are infinitely divisible; that is, the sum of an infinite number of numbers is always infinite. Though they were based on fallacies, the paradoxes remained unsolved for two millennia. In the seventeenth century AD the Scottish mathematician James Gregory showed that an infinite number of numbers can add to a finite number. Such a series of numbers is called the convergence series, which occurs when the difference between each number and the one following it becomes smaller throughout the sequence. The race between Achilles and the tortoise is not made up of a number of tiny distances but it is continuous until the end. Of course, Achilles will win the race.
Fifth
century
BC GREECE | Democritus Atomic Theory Democritus (c. 460 c. 370 BC ) |
Matter is made up of empty space and an infinite number of tiny invisible particles called atomos or atoms. |
D emocritus atomic theory was probably based on previous ideas of other Greek philosophers. It was the first scientific attempt to explain the nature of matter; however, many of Democritus assumptions have now been proved wrong.
Democritus, probably the greatest of the early Greek physical philosophers, also suggested that atoms could not be divided indefinitely into smaller parts, and that it was impossible to create new matter. He said that atoms were always in motion and as they moved about they collided with other atoms: sometimes they interlocked and held together, sometimes they rebounded from collisions. The Roman poet Lucretius (c. 94 c. 55 BC ) imagined Democritus atoms with hooks that fastened them together.
Very little is known about Democritus life, but we know all about his atomic theory from the second-century AD Greek biographer Diogenes Laertius book Lives of Eminent Philosophers . Laertius lists 73 books written by Democritus, none of which has survived. Democritus is believed to have said: I would rather discover one scientific fact than become King of Persia.
The great Greek philosopher Aristotle (384322 BC ) rejected Democritus idea of the atom and said that the matter was completely uniform and continuous. The influence of Aristotle was extraordinary. His concept of matter was basically wrong, but it was accepted for some 20 centuries until it was replaced by Daltons atomic theory (p. 65) in 1808.