ACKNOWLEDGMENTS
Besides those thanked in the introduction, I am very grateful to the many people who generously contributed their time and expertise to this book, including Carol Lane, Myrna Talman, and Jenny Arden; David Oyster, Richard Wells, Tom Weidlinger, Dennis Gutierrez, Rob McCain, Nancy Kinney, Janelle Balnicke, Judy Flannery, and Susan Racho of the Cosmos television staff; Nancy Inglis, Peter Mollman, Marylea OReilly, and Jennifer Peters of Random House; Paul west for generously lending me the title of ; and George Abell, James Allen, Barbara Amago, Lawrence Anderson, Jonathon Arons, Halton Arp, Asma El Bakri, James Blinn, Bart Bok, Zeddie Bowen, John C. Brandt, Kenneth Brecher, Frank Bristow, John Callendar, Donald B. Campbell, Judith Campbell, Elof Axel Carlson, Michael Carra, John Cassani, Judith Castagno, Catherine Cesarsky, Martin Cohen, Judy-Lynn del Rey, Nicholas Devereux, Michael Devirian, Stephen Dole, Frank D. Drake, Frederick C. Durant III, Richard Epstein, Von R. Eshleman, Ahmed Fahmy, Herbert Friedman, Robert Frosch, Jon Fukuda, Richard Gammon, Ricardo Giacconi, Thomas Gold, Paul Goldenberg, Peter Goldreich, Paul Goldsmith, J. Richard Gott III, Stephen Jay Gould, Bruce Hayes, Raymond Heacock, Wulff Heintz, Arthur Hoag, Paul Hodge, Dorrit Hoffleit, William Hoyt, Icko Iben, Mikhail Jaroszynski, Paul Jepsen, Tom Karp, Bishun N. Khare, Charles Kohlhase, Edwin Krupp, Arthur Lane, Paul MacLean, Bruce Margon, Harold Masursky, Linda Morabito, Edmond Momjian, Edward Moreno, Bruce Murray, William Murnane, Thomas A. Mutch, Kenneth Norris, Tobias Owen, Linda Paul, Roger Payne, Vahe Petrosian, James B. Pollack, George Preston, Nancy Priest, Boris Ragent, Dianne Rennell, Michael Rowton, Allan Sandage, Fred Scarf, Maarten Schmidt, Arnold Scheibel, Eugene Shoemaker, Frank Shu, Nathan Sivin, Bradford Smith, Laurence A. Soderblom, Hyron Spinrad, Edward Stone, Jeremy Stone, Ed Taylor, Kip S. Thorne, Norman Thrower, O. Brian Toon, Barbara Tuchman, Roger Ulrich, Richard Underwood, Peter van de Kamp, Jurrie J. Van der Woude, Arthur Vaughn, Joseph Veverka, Helen Simpson Vishniac, Dorothy Vitaliano, Robert Wagoner, Pete Waller, Josephine Walsh, Kent Weeks, Donald Yeomans, Stephen Yerazunis, Louise Gray Young, Harold Zirin, and the National Aeronautics and Space Administration. I am also grateful for special photographic help by Edwardo Castaeda and Bill Ray.
By Carl Sagan
Published by The Random House Publishing Group:
BROCAS BRAIN
COSMOS
THE DRAGONS OF EDEN
MURMURS OF EARTH
SHADOWS OF FORGOTTEN ANCESTORS (with Ann Druyan)
PALE BLUE DOT
BILLIONS & BILLIONS
APPENDIX 1
Reductio ad Absurdum
and the Square Root of Two
The original Pythagorean argument on the irrationality of the square root of 2 depended on a kind of argument called reductio ad absurdum, a reduction to absurdity: we assume the truth of a statement, follow its consequences and come upon a contradiction, thereby establishing its falsity. To take a modern example, consider the aphorism by the great twentieth-century physicist, Niels Bohr: The opposite of every great idea is another great idea. If the statement were true, its consequences might be at least a little perilous. For example, consider the opposite of the Golden Rule, or proscriptions against lying or Thou shalt not kill. So let us consider whether Bohrs aphorism is itself a great idea. If so, then the converse statement, The opposite of every great idea is not a great idea, must also be true. Then we have reached a reductio ad absurdum. If the converse statement is false, the aphorism need not detain us long, since it stands self-confessed as not a great idea.
We present a modern version of the proof of the irrationality of the square root of 2 using a reductio ad absurdum, and simple algebra rather than the exclusively geometrical proof discovered by the Pythagoreans. The style of argument, the mode of thinking, is at least as interesting as the conclusion:
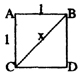
Consider a square in which the sides are 1 unit long (1 centimeter, 1 inch, 1 light-year, it does not matter). The diagonal line BC divides the square into two triangles, each containing a right angle. In such right triangles, the Pythagorean theorem holds: 12 + 12= X2. But 12 + 12 = 1 + 1 = 2, so X2 = 2 and we write x = 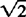 the square root of two. We assume
the square root of two. We assume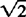 is a rational number
is a rational number 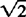 = p/q, where p and q are integers, whole numbers. They can be as big as we like and can stand for any integers we like. We can certainly require that they have no common factors. If we were to claim
= p/q, where p and q are integers, whole numbers. They can be as big as we like and can stand for any integers we like. We can certainly require that they have no common factors. If we were to claim 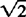 = 14/10, for example, we would of course cancel out the factor 2 and write p = 7 and q = 5, not p = 14, q = 10. Any common factor in numerator or denominator would be canceled out before we start. There are an infinite number of ps and qs we can choose. From
= 14/10, for example, we would of course cancel out the factor 2 and write p = 7 and q = 5, not p = 14, q = 10. Any common factor in numerator or denominator would be canceled out before we start. There are an infinite number of ps and qs we can choose. From 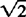 = p/q, by squaring both sides of the equation, we find that 2 = p2/q2, or, by multiplying both sides of the equation by q2, we find
= p/q, by squaring both sides of the equation, we find that 2 = p2/q2, or, by multiplying both sides of the equation by q2, we find
p2 = 2q2. (Equation 1)
p2 is then some number multiplied by 2. Therefore p2 is an even number. But the square of any odd number is odd (12 = 1, 32 = 9, 52 = 25, 72 = 49, etc.). So p itself must be even, and we can write p = 2s, where s is some other integer. Substituting for p in , we find
p2 = (2s)2 = 4s2 = 2q2
Dividing both sides of the last equality by 2, we find
q2 = 2s2
Therefore q2 is also an even number, and, by the same argument as we just used for p, it follows that q is even too. But if p and q are both even, both divisible by 2, then they have not been reduced to their lowest common factor, contradicting one of our assumptions. Reductio ad absurdum. But which assumption? The argument cannot be telling us that reduction to common factors is forbidden, that 14/10 is permitted and 7/5 is not. So the initial assumption must be wrong; p and q cannot be whole numbers; and 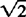 is irrational. In fact,
is irrational. In fact, 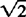 = 1.4142135
= 1.4142135
What a stunning and unexpected conclusion! How elegant the proof! But the Pythagoreans felt compelled to suppress this great discovery.
APPENDIX 2
The Five Pythagorean Solids
A regular polygon (Greek for many-angled) is a two-dimensional figure with some number, n, of equal sides. So n = 3 is an equilateral triangle, n = 4 is a square, n = 5 is a pentagon, and so on. A polyhedron (Greek for many-sided) is a three-dimensional figure, all of whose faces are polygons: a cube, for example, with 6 squares for faces. A simple polyhedron, or regular solid, is one with no holes in it. Fundamental to the work of the Pythagoreans and of Johannes Kepler was the fact that there can be 5 and only 5 regular solids. The easiest proof comes from a relationship discovered much later by Descartes and by Leonhard Euler which relates the number of faces, F, the number of edges, E, and the number of corners or vertices, V, of a regular solid:


















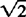 the square root of two. We assume
the square root of two. We assume