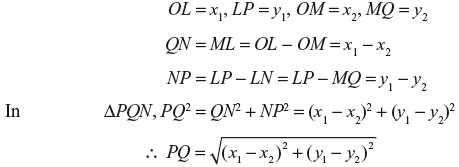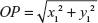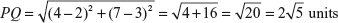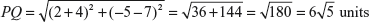P. R. Vittal [Vittal - Analytical Geometry: 2D and 3D

P. R. Vittal
Visiting Professor
Department of Statistics
University of Madras
Chennai

Chennai Delhi

P. R. Vittal was a postgraduate professor of Mathematics at Ramakrishna Mission Vivekananda College, Chennai, from where he retired as Principal in 1996. He was a visiting professor at Western Carolina University, USA, and has visited a number of universities in the USA and Canada in connection with his research work. He is, at present, a visiting professor at the Department of Statistics, University of Madras; Institute of Chartered Accountants of India, Chennai; The Institute of Technology and Management, Chennai; and National Management School, Chennai, besides being a research guide in Management Science at BITS, Ranchi.

Professor Vittal has published 30 research papers in journals of national and international repute and guided a number of students to their M.Phil. and Ph.D. degrees. A fellow of Tamil Nadu Academy of Sciences, his research topics are probability, stochastic processes, operations research, differential equations and supply chain management. He has authored about 30 books in mathematics, statistics and operations research.

To my grandchildren

Aarav and Advay

A successful course in analytical geometry must provide a foundation for future work in mathematics. Our teaching responsibilities are to instil certain technical competence in our students in this discipline of mathematics. A good textbook, as with a good teacher, should accomplish these aims. In this book, you will find a crisp, mathematically precise presentation that will allow you to easily understand and grasp the contents.

This book contains both two-dimensional and three-dimensional analytical geometry. In some of the fundamental results, vector treatment is also given and therefrom the scalar form of the results has been deduced.

The first 10 chapters deal with two-dimensional analytical geometry. In , circle and system of circles, including coaxial system and limiting points of a coaxial system, are analysed.

deal with the conic sectionsparabola, ellipse and hyperbola. Apart from their properties such as focus and directrix, their parametric equations are also explained. Special properties such as conormal points of all conics are described in details. Conjugate diameters in ellipse and hyperbola and asymptotes of a hyperbola and rectangular hyperbola are also analysed with a number of examples. A general treatment of conics and tracing of conics is also provided.

In examines the conditions for the general equation of the second degree to represent the different types of conics.

In , two special types of conicoidscone and cylinderare discussed.

A number of illustrative examples and exercises for practice are given in all these 16 chapters, to help the students understand the concepts in a better manner.

I hope that this book will be very useful for undergraduate students and engineering students who need to study analytical geometry as part of their curriculum.

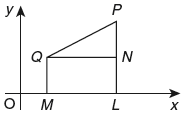
Let XOX and YOY be two fixed perpendicular lines in the plane of the paper. The line OX is called the axis of X and OY the axis of Y. OX and OY together are called the coordinate axes. The point O is called the origin of the coordinate axes. Let P be a point in this plane. Draw PM perpendicular to XOX. The distance OM is called the x-coordinate or abscissa and the distance MP is called the y-coordinate or ordinate of the point P.

If OM = x and MP = y then (x, y) are called the coordinates of the point P. The coordinates of the origin O are (0, 0). The lines XOX and YOY divide the plane into four quadrants. They are XOY, YOX, XOY and YOX. The lengths measured in the directions OX and OY are considered positive and the lengths measured in the directions OX and OY are considered negative. The nature of the coordinates in the different quadrants is as follows:

The method of representing a point by means of coordinates was first introduced by Rena Descartes and hence this branch of mathematics is called the rectangular Cartesian coordinate system.

Using this coordinate system, one can easily find the distance between two points in a plane, the coordinates of the point that divides a line segment in a given ratio, the centroid of a triangle, the area of a triangle and the locus of a point that moves according to a given geometrical law.

Let P and Q be two points with coordinates (x1, y1) and (x2, y2).

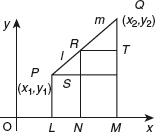
Draw PL and QM perpendiculars to the x-axis, and draw QN perpendicular to PL. Then,

Note 1.1.1: The distance of P from the origin O is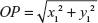

Example 1.1.1

If P is the point (4, 7) and Q is (2, 3), then

Example 1.1.2

The distance between the points P(2, 5) and Q(4, 7) is

Let the two given points be P(x1, y1) and Q(x2, y2).

Let the point R divide PQ internally in the ratio l:m. Draw PL, QM and RN perpendiculars to the x-axis. Draw PS perpendicular to RN and RT perpendicular to MQ. Let the coordinates of R be (x, y). R divides PQ internally in the ratio l:m. Then,