Geometry For Students and Parents
Roy Richard Sawyer
Copyright 2017 by Roy Richard Sawyer - All rights reserved
DEDICATION
I want to dedicate my book to my mother, who in her childhood dreamed of becoming a mathematician. Unfortunately, she did not complete her school because when she was 15, World War II prevented her from finishing her education. She had to start working and never had the opportunity to go to school again but she made a great effort so that my two brothers and I received the highest possible education. I think she would be happy to know that my geometry book is dedicated to her.
Introduction
Plane Geometry deals with points, lines, angles and polygons. A line in geometry is an indefinitely long line without a beginning or end.
The point can be the beginning of an indefinitely long line and this line is called a ray. A ray has a starting point, but no end. If the line has two end-points, it is called a segment. See Figure 1. 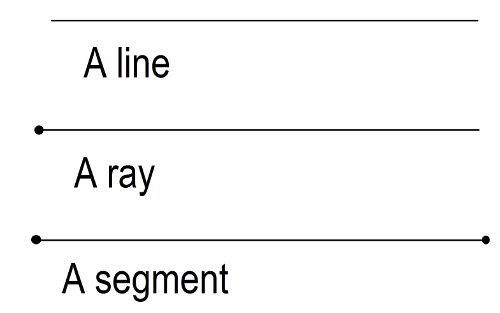 Figure 1. When two or more lines intersect with each other, they form acute and obtuse angles.
Figure 1. When two or more lines intersect with each other, they form acute and obtuse angles.
If the angle is less than 90 degrees it is referred to as acute. If the angle is greater than 90 degrees it is referred to as obtuse. Two intersecting lines form four angles. Opposite angles are called vertical angles. Angles that share one side, are called adjacent angles. See Figure 2 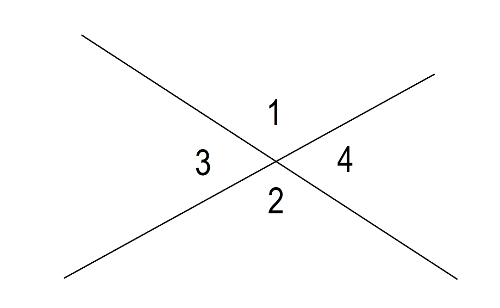 Figure 2.
Figure 2.
Vertical angles 1 and 2 are equal. Adjacent angles 1 and 4 together form a straight line and add up to 180 degrees. Angles 1 and 2 in Figure 2 are obtuse. Angles 3 and 4 are acute. If the angle is 90 degrees it is called a right angle. See Figure 3 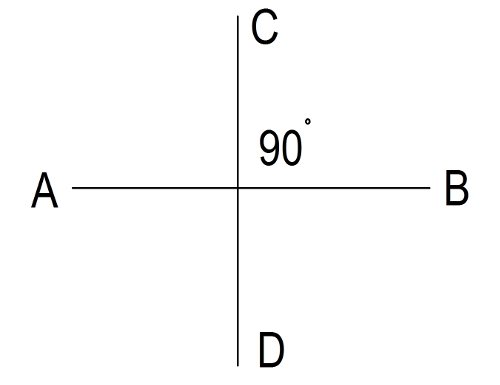 Figure 3.
Figure 3.
A right angle
Parallel Lines
If two lines never intersect with each other, they are parallel. You can see the || symbol that is used to indicate parallel lines. Per Freds theorem, if two parallel lines intersect a third line, two kinds of angles are formed: acute angles and obtuse angles. All acute angles are equal and all obtuse angles are equal. Adjacent angles add up to 180 degrees. See Figure 4
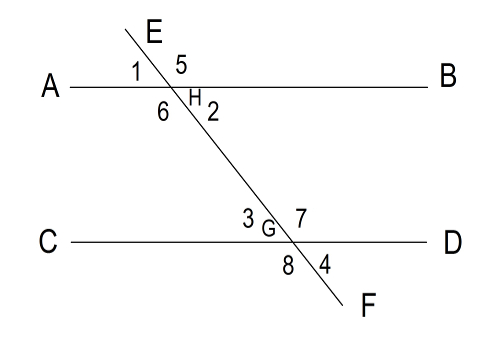
Figure 4.
AB || CD Angle 1 = 2 = 3 = 4. Angle 5 = 6 = 7 = 8 H is the point of the intercept of lines AB and EF. Similarly, G is the point of the intercept of lines CD and EF. Angles 1 and 5 are adjacent and add up to 180 degrees. Adjacent angles are: 1 and 6; 2 and 5; 6 and 2; 3 and 7; 3 and 8; 7 and 4; 8 and 4. In geometry, angles are denoted by 3 letters starting with a letter that denotes any angle side.
The angle 1 can be denoted by AHE or EHA. The angle 5 can be denoted by EHB or BHE. The angle 2 can be denoted by BHG or GHB. The angle 6 can be denoted by AHG or GHA. The angle 8 can be denoted by CGF or FGC and so on. There are three conditions that prove if two lines are parallel.
The first condition: If two lines are intersected by a third line and two inner angles adjacent to the third line add up to 180 degrees then the lines are parallel. See Figure 5. 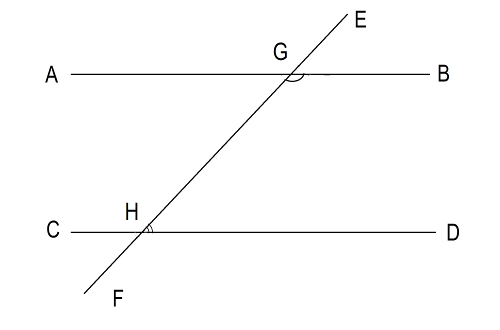 Figure 5. If angle BGH + DHG =180 then AB || CD The second condition: If two lines intersect the third line and the corresponding angles are equal, then these lines are parallel. See Figure 6.
Figure 5. If angle BGH + DHG =180 then AB || CD The second condition: If two lines intersect the third line and the corresponding angles are equal, then these lines are parallel. See Figure 6. 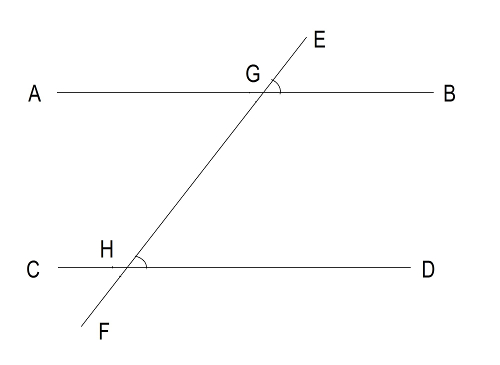 Figure 6.
Figure 6.
If angle BGE=DHG then AB || CD The third condition: If two lines intersect the third line and the crosswise lying angles are equal then these two lines are parallel. See Figure 7 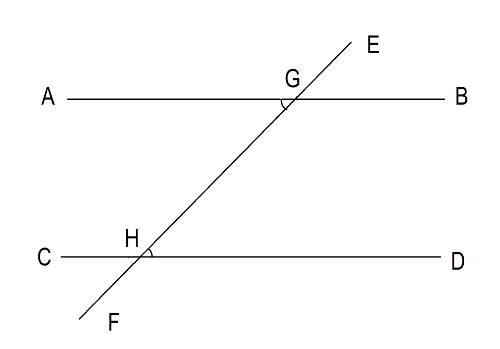 Figure 7.If angle AGH= DHG then AB || CD If two lines intersect and form an angle of 90 degrees, they are perpendicular to each other.
Figure 7.If angle AGH= DHG then AB || CD If two lines intersect and form an angle of 90 degrees, they are perpendicular to each other.
In this case, all four angles are equal, and each angle is equal to 90 degrees. See Figure 8. The _ | _ symbol is used to indicate that the lines are perpendicular. AB _ | _ CD  Figure 8. Perpendicular lines
Figure 8. Perpendicular lines
Polygons
Polygons are two-dimensional Figures made of a variable number of segments.
For example, polygons made of 3 line segments are called triangles. Polygons made of 4 line segments are called quadrilaterals. Polygons made of five line segments are called pentagons. Polygons made of six line segments are called hexagons. If all the sides of the polygon are equal, the polygon is called a regular polygon: equilateral triangle, regular quadrilateral, regular pentagon and a regular hexagon. 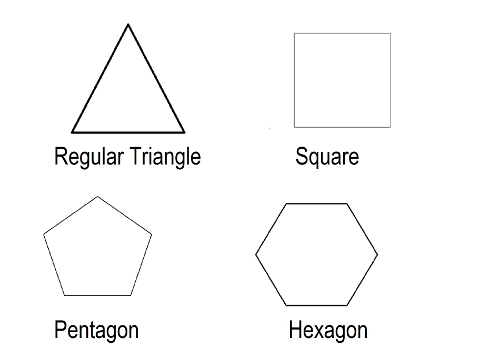 Figure 9.
Figure 9.  Figure 9.
Figure 9.
Regular polygons.
Triangles
Now lets start with triangles. Triangles have three sides and three angles. There are three types of triangles. A triangle having three sides of equal length is called an equilateral triangle. A triangle having two sides of equal length is called an isosceles triangle.
A triangle having three unequal sides is called a scalene triangle. See Figure 10. 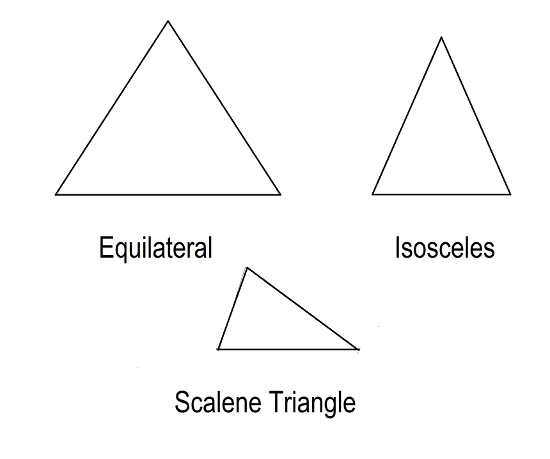 Figure 10. Different Types of Triangles. The sum of the inner angles of a triangle equal 180 degrees.
Figure 10. Different Types of Triangles. The sum of the inner angles of a triangle equal 180 degrees. 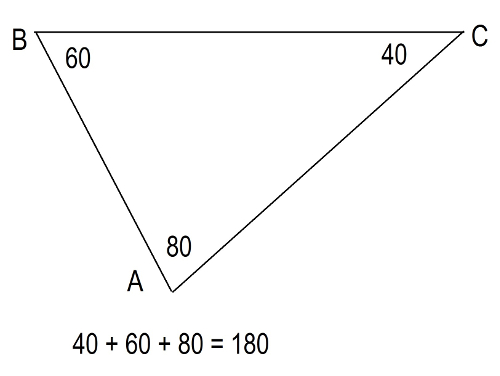 Figure 11.
Figure 11.  Figure 11.
Figure 11.
The sum of the inner angles of a triangle. BAC + ABC + ACB = 180 If a triangle has all three angles less than 90 degrees, it is called an acute triangle. If a triangle has one angle which equals 90 degrees, it is called a right triangle. If a triangle has one angle that is greater than 90 degrees, it is called an obtuse triangle. See Figure 12. 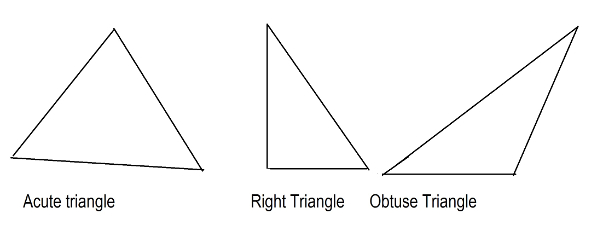 Figure 12.
Figure 12.
When you want to refer to an angle, you denote it by 3 letters starting with a letter that denotes any angle side. For example, you can denote the angle ABC as CBA. Either way is correct, even though the first one may sound nicer. An angle, which is formed by one side of a triangle and the continuation of the adjacent side of the same triangle, is equal to the sum of the internal, not adjacent, angles of the triangle. See Figure 13. 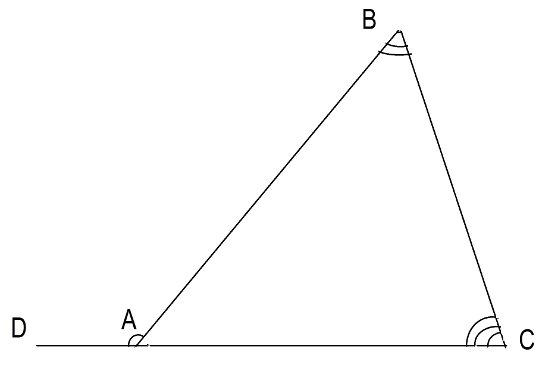













 Figure 1. When two or more lines intersect with each other, they form acute and obtuse angles.
Figure 1. When two or more lines intersect with each other, they form acute and obtuse angles. Figure 2.
Figure 2. Figure 3.
Figure 3. Figure 4.
Figure 4.  Figure 5. If angle BGH + DHG =180 then AB || CD The second condition: If two lines intersect the third line and the corresponding angles are equal, then these lines are parallel. See Figure 6.
Figure 5. If angle BGH + DHG =180 then AB || CD The second condition: If two lines intersect the third line and the corresponding angles are equal, then these lines are parallel. See Figure 6.  Figure 6.
Figure 6. Figure 7.If angle AGH= DHG then AB || CD If two lines intersect and form an angle of 90 degrees, they are perpendicular to each other.
Figure 7.If angle AGH= DHG then AB || CD If two lines intersect and form an angle of 90 degrees, they are perpendicular to each other. Figure 9.
Figure 9.  Figure 10. Different Types of Triangles. The sum of the inner angles of a triangle equal 180 degrees.
Figure 10. Different Types of Triangles. The sum of the inner angles of a triangle equal 180 degrees.  Figure 11.
Figure 11.  Figure 12.
Figure 12.