Famous Problems
of Geometry
and How to Solve Them
BENJAMIN BOLD
DOVER PUBLICATIONS, INC.
New York
Copyright 1969 by Benjamin Bold.
All rights reserved.
This Dover edition, first published in 1982, is an unabridged and slightly corrected republication of the work originally published in 1969 by Van Nostrand Reinhold Company, N.Y., under the title Famous Problems of Mathematics: A History of Constructions with Straight Edge and Compass.
Library of Congress Cataloging in Publication Data
Bold, Benjamin.
Famous problems of geometry and how to solve them.
Reprint. Originally published: Famous problems of mathematics. New York : Van Nostrand Reinhold, 1969.
1. GeometryProblems, Famous. I. Title.
QA466.B64 1982 516.204 81-17374
ISBN 0-486-24297-8 AACR2
Manufactured in the United States by Courier Corporation
24297813
www.doverpublications.com
To My Wife, CLAIRE,
Whose Assistance and Encouragement
Made this Book Possible
Foreword
IN JUNE OF 1963 a symposium on Mathematics and the Social Sciences was sponsored by the American Academy of Political and Social Sciences. One of the contributions was by Oscar Morgenstern, who, together with John Von Neumann, had written the book The Theory of Games and Economic Behavior. This book stimulated the application of mathematics to the solution of problems in economics, and led to the development of the mathematical Theory of Games. Dr. Morgensterns contribution to the Symposium was called the Limits of the Uses of Mathematics in Economics. I shall quote the first paragraph of this article.
Although some of the profoundest insights the human mind has achieved are best stated in negative form, it is exceedingly dangerous to discuss limits in a categorical manner. Such insights are that there can be no perpetuum mobile, that the speed of light cannot be exceeded, that the circle cannot be squared using ruler and compasses only, that similarly an angle cannot be trisected, and so on. Each one of these statements is the culmination of great intellectual effort. All are based on centuries of work and either on massive empirical evidence or on the development of new mathematics or both. Though stated negatively, these and other discoveries are positive achievements and great contributions to human knowledge. All involve mathematical reasoning; some are, indeed, in the field of pure mathematics, which abounds in statements of prohibitions and impossibilities.
The above quotation states clearly and forcefully the purpose of this book. Why does mathematics abound in statements of prohibitions and impossibilities? Why are the solutions of such problems as squaring the circle and trisecting an angle considered to be profound insights and great contributions to human knowledge? Why were centuries of great intellectual effort required to solve such seemingly simple problems? And, finally, what new mathematics had to be developed to resolve these problems? I hope you will find the answers to these questions as you read this book.
The outstanding achievement of the Greek mathematicians was the development of a postulational system. Despite the flaws and defects of euclidean geometry as conceived by the ancient Greeks, their work serves as a model that is followed even up to the present day.
In a postulational system one starts with a set of unproved statements (postulates) and deduces (by means of logic) other statements (theorems). Two of the postulates of euclidean plane geometry are:
1) given any two distinct points, there exists a unique line through the two points.
2) given a point and a length, a circle can be constructed with the given point as center and the given length as radius.
These two postulates form the basis for euclidean constructions (constructions using only an unmarked straight edge and compasses). With these two instruments the Greek mathematicians were able to perform many constructions; but they also were unsuccessful in many instances. Thus, they were able to bisect any given angle, but were unable to trisect a general angle. They were able to construct a square equal in area to twice a given square, but were unable to duplicate a cube. They were able to construct a square equal in area to a given polygon, but were unable to square a circle. They were able to construct regular polygons of 3, 4, 5, 6, 8 and 10 sides, but were unable to construct regular polygons of 7 or 9 sides. Before the end of the 19th century, mathematicians had supplied answers to all of these problems of antiquity. The purpose of this book is to show how these problems were eventually solved.
Why were the Greek mathematicians unable to solve these problems? Why was there a lapse of about two thousand years before solutions to these problems were found?
The mathematical efforts of the Greeks were along geometric lines. The concentration on geometry, and the resulting neglect of algebra, was due to the following situation:
The Pythagorean theorem tells us that, if the length of a side of a square is one unit, the length of the diagonal is 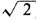 units. What kind of number is
units. What kind of number is 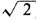 ? The Greek mathematicians, up to this point, were able to express all their results in terms of integers. Fractions, or rational numbers, are ordered pairs of integersi.e., numbers of the form a/b, where a and b are integers, b 0. No matter how they tried, the Greeks were unable to express
? The Greek mathematicians, up to this point, were able to express all their results in terms of integers. Fractions, or rational numbers, are ordered pairs of integersi.e., numbers of the form a/b, where a and b are integers, b 0. No matter how they tried, the Greeks were unable to express 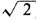 in terms of integers. As you already know, it can be proven that
in terms of integers. As you already know, it can be proven that 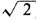 is irrational, and it was not until the 19th century that a satisfactory theory of irrationals was developed.
is irrational, and it was not until the 19th century that a satisfactory theory of irrationals was developed.
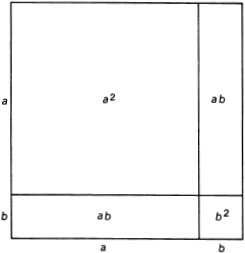
Because of the lack of such a theory, the course of Greek mathematics took a geometric turn. Thus, when the Greeks wished to expand (a + b)2, they proceeded geometrically as follows:
(a + b)2 = a2 + 2ab + b2
As we shall show later the solution of the construction problems involves well developed algebraic techniques, and in fact, it was not until algebra and analytic geometry were developed in the 17th century by Vieta, Descartes, Fermat, and others, that procedures were obtained that could be used in a successful attack on the construction problems.
Famous Problems
of Geometry
and How to Solve Them
CHAPTER I
Achievement of the Ancient Greeks
USING GEOMETRIC THEOREMS, the Greek mathematicians were able to construct any desired geometric element that could be derived by a finite number of rational operations and extractions of real square roots from the given elements. To illustrate: Suppose we are given the elements a, b, and the unit element. The Greeks could construct a + b, ab, ab, a/b, a2, and 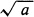 .
.
PROBLEM SET IA
Construct a + b and ab, using the given line segments. The following diagram shows how to construct ab. If EG is constructed parallel to DF, then













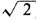 units. What kind of number is
units. What kind of number is 
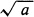 .
.