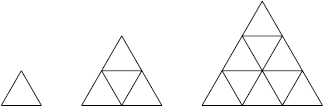
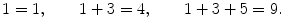LitArk » Books » Children

Francis Borceux - An Axiomatic Approach to Geometry: Geometric Trilogy I

Here you can read online Francis Borceux - An Axiomatic Approach to Geometry: Geometric Trilogy I full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2013, publisher: Springer, genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:

Romance novel Science fiction Adventure Detective Science History Home and family Prose Art Politics Computer Non-fiction Religion Business Children Humor

Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.

Book:
An Axiomatic Approach to Geometry: Geometric Trilogy I
Author:
Francis Borceux
Publisher:
Springer
Genre:
Books / Children
Year:
2013
Rating:
5 / 5
Favourites:
Add to favourites
Your mark:
- 100
- 1
- 2
- 3
- 4
- 5

Description
Author's other books
Similar books

An Axiomatic Approach to Geometry: Geometric Trilogy I: summary, description and annotation

We offer to read an annotation, description, summary or preface (depends on what the author of the book "An Axiomatic Approach to Geometry: Geometric Trilogy I" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.

Focusing methodologically on those historical aspects that are relevant to supporting intuition in axiomatic approaches to geometry, the book develops systematic and modern approaches to the three core aspects of axiomatic geometry: Euclidean, non-Euclidean and projective. Historically, axiomatic geometry marks the origin of formalized mathematical activity. It is in this discipline that most historically famous problems can be found, the solutions of which have led to various presently very active domains of research, especially in algebra. The recognition of the coherence of two-by-two contradictory axiomatic systems for geometry (like one single parallel, no parallel at all, several parallels) has led to the emergence of mathematical theories based on an arbitrary system of axioms, an essential feature of contemporary mathematics.

This is a fascinating book for all those who teach or study axiomatic geometry, and who are interested in the history of geometry or who want to see a complete proof of one of the famous problems encountered, but not solved, during their studies: circle squaring, duplication of the cube, trisection of the angle, construction of regular polygons, construction of models of non-Euclidean geometries, etc. It also provides hundreds of figures that support intuition.

Through 35 centuries of the history of geometry, discover the birth and follow the evolution of those innovative ideas that allowed humankind to develop so many aspects of contemporary mathematics. Understand the various levels of rigor which successively established themselves through the centuries. Be amazed, as mathematicians of the 19th century were, when observing that both an axiom and its contradiction can be chosen as a valid basis for developing a mathematical theory. Pass through the door of this incredible world of axiomatic mathematical theories!

Francis Borceux: author's other books

Who wrote An Axiomatic Approach to Geometry: Geometric Trilogy I? Find out the surname, the name of the author of the book and a list of all author's works by series.

An Axiomatic Approach to Geometry: Geometric Trilogy I — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "An Axiomatic Approach to Geometry: Geometric Trilogy I" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓

↑

Reset

Interval:

↓

↑

Bookmark:

Make

Francis Borceux An Axiomatic Approach to Geometry 2014 Geometric Trilogy I 10.1007/978-3-319-01730-3_1

Springer International Publishing Switzerland 2014

1. Pre-Hellenic Antiquity

Francis Borceux 1

(1)

Universit catholique de Louvain, Louvain-la-Neuve, Belgium

Abstract

Already two millenniums before Christ, a substantial geometric knowledge exists: results like the Pythagoras or the Thales intercept theorem are known of the Egyptians or Mesopotamians, long before the Greek mathematicians provide a formal proof of these. Various approximate formulas for computing lengths, areas or volumes are also known.

This very short chapter is intended only to give an overview of some of the first geometric ideas which arose in various civilizations before the influence of the systematic work of the Greek geometers. So pre-Hellenic should be understood here as before the Greek influence.

From this pre-Hellenic antiquity, we know of various works due to the Egyptians and the Babylonians. Indeed, these are the only pre-Hellenic civilizations which have produced written geometric documents that have survived to the present day.

It should nevertheless be mentioned here that some works in China and Indiaposterior to the golden age of geometry in Greeceare considered by some historians as pre-Hellenic in the sense of being absent of Greek influence. But not all specialists agree on this point. Therefore we choose in this book to mention these developments at their chronological place, after the Greek period.

1.1 Prehistory

Prehistory is characterized by the absence of writing. In those days, the transmission of knowledge was essentially oral. But nowadays, we no longer hear those voices. Therefore prehistory remains as silent about geometry as it is about all other aspects of human life. The best that we can do is to rely on archaeological discoveries and try to interpret the various cave pictures and objects that have been found.

The first geometric pictures date from 25000 BC. They already indicate some mastering of the notions of symmetry and congruence of figures. Some other objects of the same period show evidence of the first arithmetical developments, such as the idea of counting.

Particularly intriguing is the picture in Fig. : it seems to be evident that the prehistoric artist did not just want to draw a nice picture: he/she wanted to emphasize some mathematical discovery. Indeed, looking at this picture, we notice at once that:

doubling the side of the triangle multiplies the area by 4; tripling the side of the triangle multiplies the area by 9;
counting the number of small triangles on each line we observe that

The oldest written documents that we know concerning geometry already mention the corresponding general results:

multiplying the lengths by n results in multiplying the areas by n 2;
the sum of the n first odd numbers is equal to n 2.

To what extent was the prehistoric artist aware of these theorems? We shall probably never know.

Fig. 1.1

A tradition claims that the origin of arithmetic and geometry is to be found in the religious rituals of our ancestors: they were fascinated by the properties of some forms and some numbers, to which they attributed magical powers. By introducing such magical forms and numbers into their rituals they might perhaps draw the benediction of their gods.

Another tradition, reported by Herodotus (c. 484 BCc. 425 BC) presents geometry as the precious daughter of the caprices of the Nile. Legendary Pharaoh Sesostris (around 1300 BC; but probably a compound of Seti and Ramesses II ) had, claims Herodotus, distributed the Egyptian ground between the (by which we understand some few privileged) inhabitants. The annual floods of the Nile valley, the origin of its fertility but also of many dramatic events, made it necessary to devise practical methods of retracing the limits of each estate after each flood. These methods were based on triangulation and probably made use of some special instances of Pythagoras theorem for constructing right angles. For example, the fact that a triangle with sides 3, 4, 5 has a right angle seems to have been known at least since 2000 BC.

But the Nile valley certainly does not have the hegemony of early developments of mathematics, not even in Africa: the discovery in 1950 of the Ishango bone in Congo, dating from 22000 BC, is one of the oldest testimonies of some mathematical activity. And various discoveries in Europe, India, China, Mesopotamia, and so on, indicate thatat different levels of developmentmathematical thought was present in many places in the world during antiquity.

However, up to now, modest prehistory has unveiled very little of its personal relations with geometry.

1.2 Egypt

The oldest mathematical papyrus which has reached us is the so-called Moscow papyrus , most likely written around 1850 BC. But our main knowledge of Egyptian mathematics during high antiquity comes from a more extended papyrus copied by the scribe Ahmes around 1650 BC. These papyri contain the solutions to many arithmetical and geometrical problems whose elaboration, according to Ahmes, dates back to 2000 BC.

The Moscow papyrus is also called the Golenischev Mathematical Papyrus , after the Egyptologist Vladimir Golenishchev who bought the papyrus in Thebes around 1893. The papyrus later entered the collection of the Pushkin State Museum of Fine Arts in Moscow, where it remains today. The Ahmes papyrus is often referred to as the Rhind papyrus , so named after Alexander Henry Rhind , a Scottish antiquarian, who purchased the papyrus in 1858 in Luxor, Egypt. The papyrus was apparently found during illegal excavations on the site of the mortuary temple of Pharaoh Ramesses II. It is kept at the British Museum in London .

For example, Problem 51 of the Ahmes papyrus shows that

The area of an isosceles triangle is equal to the height multiplied by half of the base .

The explanation is a cut and paste argument as in Fig.. Cut the triangle along its height; reverse one piece, turn it upside down and glue both pieces together; you get the rectangle on the right.

Fig. 1.2

An analogous argument is used in Problem 52 to show that

The area of an isosceles trapezium is equal to the height multiplied by half the sum of the bases .

See Fig. , which is again a proof in itself. At least, it is a proof in the spirit of the time: in any case, an argument based on congruences of figures.

Fig. 1.3

However, let us stress that the Egyptians did not have a notion of what a theorem or a formal proof is, in the mathematical sense of the term. In particular, they did not make a clear distinction between a precise result and an approximative one. For example, one finds in Egyptian documents the following strange rule to compute the area of a quadrilateral:

Light

Font size:

↓

↑

Reset

Interval:

↓

↑

Bookmark:

Make

Similar books «An Axiomatic Approach to Geometry: Geometric Trilogy I»

Look at similar books to An Axiomatic Approach to Geometry: Geometric Trilogy I. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.

Maciej Dunajski

Geometry: A Very Short Introduction

Wladimir-Georges Boskoff

A Mathematical Journey to Relativity: Deriving Special and General Relativity with Basic Mathematics

Tumarkin

Axiomatic

Stahl

Geometry from Euclid to Knots

Clayton W. Dodge

Euclidean Geometry and Transformations

Leonard M. Blumenthal

A Modern View of Geometry

V. I. Arnold

Mathematical Methods of Classical Mechanics

Lawson

Algebra & geometry: an introduction to university mathematics

C. R. Wylie Jr.

Introduction to Projective Geometry

Saul Stahl

Geometry from Euclid to Knots

Melvin Hausner

A Vector Space Approach to Geometry

Irving Adler

A New Look at Geometry

Reviews about «An Axiomatic Approach to Geometry: Geometric Trilogy I»

Discussion, reviews of the book An Axiomatic Approach to Geometry: Geometric Trilogy I and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.