A VECTOR SPACE
APPROACH
TO GEOMETRY

Melvin Hausner
Professor of Mathematics
New York University DOVER PUBLICATIONS, INC. Mineola, New York
Copyright Copyright 1965 by Melvin Hausner All rights reserved under Pan American and International Copyright Conventions.
Bibliographical Note This Dover edition, first published in 1998, is an unabridged republication of the work originally published in the Prentice-Hall Mathematics Series by Prentice-Hall, Inc., Englewood Cliffs, N.J., in 1965.
Library of Congress Cataloging-in-Publication Data Hausner, Melvin, 1928 A vector space approach to geometry / Melvin Hausner. p. cm.
Originally published: Englewood Cliffs : Prentice-Hall, 1965. Includes index. ISBN 0-486-40452-8 (pbk.) 1. Geometry, Algebraic. 2. I. Title. Title.
QA564.H3 1998 516.65dc21 98-24686 CIP Manufactured in the United States by Courier Corporation
40452804 www.doverpublications.com PREFACE This book is the outgrowth of a one year in-service course for high school teachers of mathematics, which the author gave at New York University in 1961 and again in 1963. For the most part, it consists of an exploration of the effect that geometry and linear algebra have on each other. In addition, it attempts on an elementary, but nontrivial level, to present the interrelationships of geometry with other branches of mathematics and science, including physics, probability, analysis, and group theory. All of the linear algebra which is required for the text is developed here. It is not intended that the material in this book be a first course in geometry, or in algebra. Nor is it intended to be a Grand Scheme to inject some New Math into a curriculum.
Rather, it is meant to show that geometry need not necessarily be considered a field unto itself; that it can be helped in its development and in its understanding by foreign ideas such as algebra and the center of mass. Conversely, the geometric viewpoint in various subjects (for example, probability, determinant theory, function spaces) can aid greatly in understanding them. Thus, the interplay between geometry and other subjects enriches them both. The reader of this book will find it quite possible to omit many sections without affecting his understanding of the later sections. The core of the book, however, will be found in for the second term. Although much algebra is used and developed here, this book is basically a geometry text, and no serious attempt has been made to give a totally axiomatic account of vector spaces.
Thus, ordinary algebra is taken for granted, and the reader is encouraged to proceed naturally rather than to question each algebraic step in a proof. The author is happy to express his gratitude to Professor Walter Prenowitz for first showing him that linear algebra had, after all, something to do with geometry; to Professor Jacob T. Schwartz who outlined the original course in the period of five minutes; to the National Science Foundation for its willingness to sponsor this course and similar courses; and finally to a large, but finite, staff of efficient secretaries at the Courant Institute of Mathematical Sciences who typed the notes which formed the basis of this text. MELVIN HAUSNER CONTENTS A VECTOR SPACE
APPROACH
TO GEOMETRY THE CENTER OF MASS1.1 INTRODUCTION Many geometric facts may be made quite vivid and intuitive with the help of the physical notion of the center of mass. It is the purpose of this chapter to illustrate some of the techniques involved. But, lest the reader jump to hasty conclusions, we offer a note of caution.
It should not be thought that the methods of this chapter merely give physical proofs. Rather, the center of mass may be used as motivation for certain parts of geometry. Furthermore, as we shall see, this notion can be made mathematically precise. To consider a rough analogy, geometry may be defined and taught without a single picture. Doing so may be considered by some to be a great advance, but it is wrong to consider geometry with pictures as merely giving artistic proofs. 1.2 SOME PHYSICAL ASSUMPTIONS AND CONVENTIONS A mass-point is visualized as a particle having a certain mass m located at a point P of space. 1.2 SOME PHYSICAL ASSUMPTIONS AND CONVENTIONS A mass-point is visualized as a particle having a certain mass m located at a point P of space.
It is, of course, an idealized physical notion. We shall be concerned with bodies consisting of finitely many mass-points. These notions are used by physicists every day. Thus a ball is often idealized as a mass-point, and in astronomical contexts it is perfectly reasonable to take the earth and stars as mass-points. Furthermore, a large solid mass is approximated by cutting it up into (finitely many) small pieces and considering each part as a mass-point. For many purposes, a solid body of total mass m may be replaced by a single mass-point of mass m, located at the center of mass of the body.
We are going to make various assumptions about the center of mass. These will be made quite explicit in , but for the present we prefer to work intuitively. An especially simple mass consists of two mass-points located at A and B with masses m1 and m2, respectively, as in ). Thus, 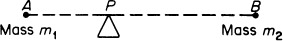 FIGURE 1.1
FIGURE 1.1 FIGURE 1.2
FIGURE 1.2 This has the effect of pulling P closer to B when the mass of B gets larger. (If m2 increases, so does AP.) Therefore, by the device of mass-points, we shall be able to deal with points P on a segment AB which divide AB in a given ratio. We may easily remember the rule where we read AP/PB = 5/3 and we say that P divides AB in the ratio 5/3.
This has the effect of pulling P closer to B when the mass of B gets larger. (If m2 increases, so does AP.) Therefore, by the device of mass-points, we shall be able to deal with points P on a segment AB which divide AB in a given ratio. We may easily remember the rule where we read AP/PB = 5/3 and we say that P divides AB in the ratio 5/3.
The numbers 5 and 3 do not represent the distances AP and PB but give the ratio AP/PB, and any proportional numbers will do as well. 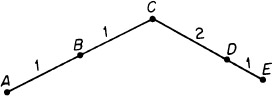 FIGURE 1.3 It is convenient to use a similar device for broken lines. In this case, the numbers along a line refer only to ratios along that line. Thus, in rather than CD = 2ED. Thus we make sure that the directions CD and DE are the same. If a mass-point is located at A and has mass m, we shall refer to the mass-point mA.
FIGURE 1.3 It is convenient to use a similar device for broken lines. In this case, the numbers along a line refer only to ratios along that line. Thus, in rather than CD = 2ED. Thus we make sure that the directions CD and DE are the same. If a mass-point is located at A and has mass m, we shall refer to the mass-point mA.
Thus we may refer to a system of mass-points 3A, 4B, 9C instead of the more cumbersome system of mass-points located at A, B, C with masses 3, 4, and 9, respectively. When we wish to replace them with a single mass-point located at their center of mass, we replace them with 16X, where X is the center of mass of this system, and 16 = 3 + 4 + 9 is the total mass. In the next few sections, we shall learn how to find such a center of mass. 1.3 PHYSICAL MOTIVATIONS IN GEOMETRY













 Melvin Hausner Professor of Mathematics
Melvin Hausner Professor of Mathematics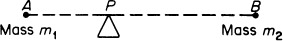 FIGURE 1.1
FIGURE 1.1 FIGURE 1.2
FIGURE 1.2 This has the effect of pulling P closer to B when the mass of B gets larger. (If m2 increases, so does AP.) Therefore, by the device of mass-points, we shall be able to deal with points P on a segment AB which divide AB in a given ratio. We may easily remember the rule where we read AP/PB = 5/3 and we say that P divides AB in the ratio 5/3.
This has the effect of pulling P closer to B when the mass of B gets larger. (If m2 increases, so does AP.) Therefore, by the device of mass-points, we shall be able to deal with points P on a segment AB which divide AB in a given ratio. We may easily remember the rule where we read AP/PB = 5/3 and we say that P divides AB in the ratio 5/3. FIGURE 1.3 It is convenient to use a similar device for broken lines. In this case, the numbers along a line refer only to ratios along that line. Thus, in rather than CD = 2ED. Thus we make sure that the directions CD and DE are the same. If a mass-point is located at A and has mass m, we shall refer to the mass-point mA.
FIGURE 1.3 It is convenient to use a similar device for broken lines. In this case, the numbers along a line refer only to ratios along that line. Thus, in rather than CD = 2ED. Thus we make sure that the directions CD and DE are the same. If a mass-point is located at A and has mass m, we shall refer to the mass-point mA.